개인적인 호기심에서 진행한 연구입니다. 제가 잘못 알고 있는 점이나 수정•보완이 필요한 부분은 댓글로 알려주시면 감사드리겠습니다. 그럼 시작하겠습니다.
들어가는 글
앞선 포스팅인 ‘1편-공원일몰제’에서 해당 제도가 가진 심각성과 그에 대한 해결책인 수직빌딩숲에 대해 살펴보았다. 앞선 포스팅을 보면 선정된 부지에 한해서 수직빌딩숲을 건설하는 것이 매입금액과 녹지 손실의 부담을 꽤 잘 줄일 수 있음을 느낄 수 있을 것이다. 그렇다면 수직빌딩숲을 지었을 때 얼마만큼의 미세먼지가 줄어들 수 있을까? 의문을 해소하기 위해 딥러닝과 수목의 미세먼지 저감 효과를 이용해서 수직빌딩숲의 미세먼지 저감 효과에 대해 알아보자.
1. 모델 생성을 위한 데이터셋 구축
딥러닝 및 머신러닝을 통한 미세먼지 예측 모델을 만들기 전에, 알맞은 데이터셋을 만들어 미세먼지 관련 EDA를 진행하는 것이 올바른 순서라고 판단했다. 따라서 미세먼지 데이터셋을 생성하고 이를 이용하여 EDA를 진행해보겠다.
1-1. 미세먼지 데이터셋 생성

미세먼지를 생성하는 물질은 ‘전구물질’이라 불린다. 그리고 이 전구물질에는 대표적으로 SO2, NO2, CO, O3 등 자동차와 공장의 매연, 그리고 석탄의 연소 시에 나오는 원소들이다. 실제로 전구물질간 화학작용으로 발생하는 미세먼지의 양은 전체 미세먼지 양의 2/3에 해당할 정도로 많은 양이다.
또한 미세먼지는 계절성이 뚜렷하다. 이는 우리의 귀납적 관찰과 봄, 겨울만 되면 언론에서 쏟아내는 정보만 보더라도 알 수 있을 것이라 생각한다. 따라서 미세먼지 EDA를 위한 독립변수는 우선 ‘전구물질’ + ‘날씨 변수’로 선정했다.
- 기간 : 2010년 01월 01일 ~ 2018년 09월 30일
- 전구물질 : SO2, CO, O3, NO2
- 기상 변수 : 평균 온도, 최고 온도, 최저 온도, 평균 습도, 최저 습도, 최고 습도, 평균 풍속, 최고 풍속, 강우량
- 종속 변수 : PM10
데이터셋은 2010년 1월 1일부터 2018년 9월 30일까지 길이가 3,414이며, 차원은 종속변수(PM10)는 1차원, 독립변수는 13차원이다.
2. 이상치(Outlier) 탐지 및 제거
이상치(outlier)란, 관측된 데이터 범위에서 매우 크거나 작은 값으로 데이터 범위를 많이 벗어난 값을 일컫는다. 만약 이상치를 제거하지 않으면 EDA에서 잘못된 결과가 나올 수 있다. 따라서 이를 사전에 방지하고자 이상치 제거를 진행했다.
2-1. Standard Scale VS Robust Scale
2-1-1. Standard Scale
평균은 0, 표준편차는 1이 되도록 변환해준다. 가장 일반적으로 사용되는 스케일링 기법이다.
1
2
3
4
5
6
7
8
9
10
from sklearn.preprocessing import StandardScaler
scale_data = data.iloc[:, range(0, len(data.columns)-2)]
scaler = StandardScaler()
scaler.fit(scale_data)
scale_data_scaled_standard = scaler.transform(scale_data)
scale_data_scaled_standard = pd.DataFrame(scale_data_scaled_standard).describe()
scale_data_scaled_standard.columns = scale_data.columns
scale_data_scaled_standard = round(scale_data_scaled_standard)
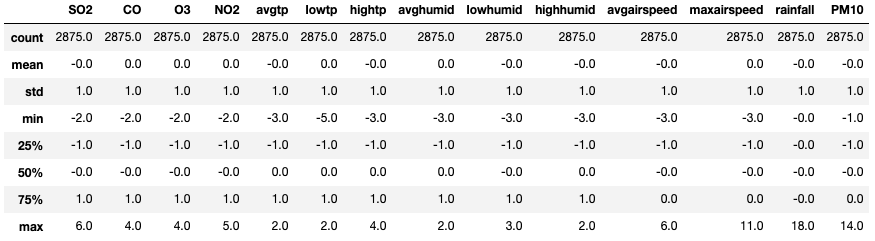
위의 데이터셋을 보면 StandardScaler에 의해 모든 변수의 평균은 0, 표준편차는 1로 변환된것을 볼 수 있다. 이제 Robust Scale로 변환해보자.
2-1-2. Robust Scale
Robust Scale은 중앙값(median)dl 0, IQR(interquartile range)이 1이 되도록 변환해준다. Roubust Scale은 이상치의 영향을 최소화한 기법으로 Standard Scale보다 표준화 값을 더 넓게 분포시킨다는 특징이 있다.
1
2
3
4
5
6
7
8
9
10
from sklearn.preprocessing import StandardScaler
scale_data = data.iloc[:, range(0, len(data.columns)-2)]
scaler = RobustScaler()
scaler.fit(scale_data)
scale_data_scaled_robust = robust_scaler.transform(scale_data)
scale_data_scaled_robust = pd.DataFrame(scale_data_scaled_robust).describe()
scale_data_scaled_robust.columns = scale_data.columns
scale_data_scaled_robust = round(scale_data_scaled_robust)
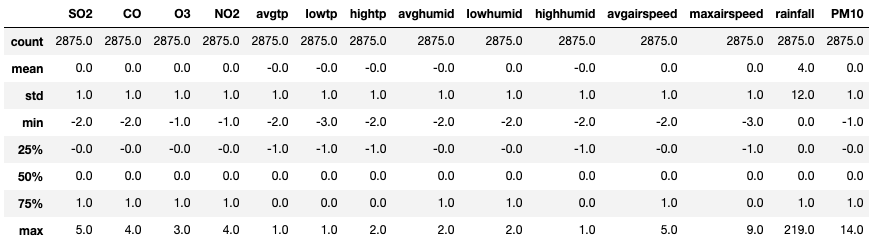
위의 Roubust Sclae을 보면 중앙값인 ‘50%’가 0임을 알 수 있고 ‘25%’~’75%’까지의 거리인 IQR이 1임을 알 수 있다. 두 스케일 변환의 가장 큰 차이점은 분산인 ‘std’인데 StandardSclaer로 변환한 것과는 다르게 RobustScaler로 변환된 값에서는 유독 강우량(rainfall)의 분산이 매우 크게 나타남을 알 수 있다. 그렇다면 이상치 제거 과정을 통해 위의 두 Scale 중 어느것을 사용하는게 더 적절한지 살펴보자.
2-2. Isolation Forest
Isolation Forest는 Regression Tree 기반으로 데이터를 계속 Split하여 데이터 관측치를 고립시키는 방법이다. 이상치일 수록 데이터가 크게 벗아나 있기 때문에 Split하는 과정에서 빨리 고립된다. 이와 반대로 정상적인 데이터는 데이터 범위 내에 있기 때문에 Split과정을 여러번 거친 후에야 고립된다. 이를 그림으로 보면 쉽게 이해할 수 있다.
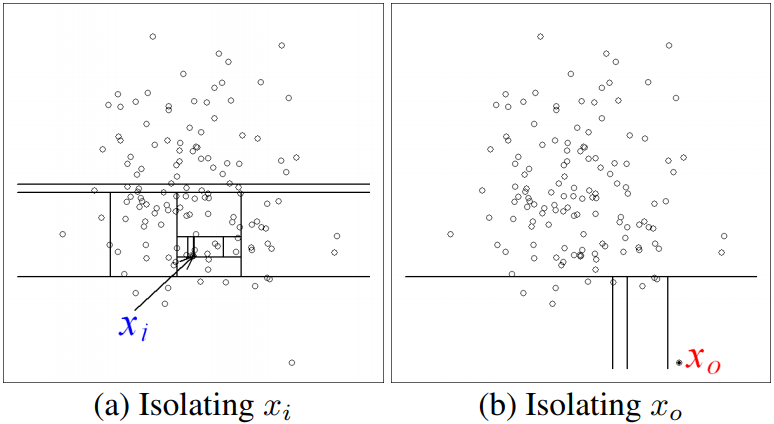
위의 그림을 보면 이상치인 X0는 데이터 범위에서 크게 벗어나 있기 때문에 몇번의 Split만으로도 쉽게 고립됨을 알 수 있다. 이와 반면에 정상치인 Xi는 데이터 범위 내에 있기 때문에 많은 Split과정을 거쳐야 고립됨을 볼 수 있다.
2-2-1. Isolation Forest을 왜 사용할까?
- 다차원의 데이터셋에서 효율적으로 작동하는 이상치 제거 방법
- 의사결정트리 기반의 이상치 탐지 기법
- 의사결정트리의 샘플 분포를 여러개 뽑아 앙상블 모델로 변환하여 안정적인 이상치 탐지 및 제거 가능
- 군집기반 이상탐지 알고리즘에 비해 월등한 실행 성능
- 전체 데이터가 아닌 데이터를 샘플링해서 사용하기 때문에 ‘Swamping’과 ‘Masking’ 문제를 예방할 수 있다.
‘Swamping’ : 정상치가 이상치에 가까운 경우 정상치를 이상치로 잘못 분류하는 현상
‘Masking’ : 이상치가 군집화되어 있으면 정상치로 잘못 분류하는 현상
2-2-2. Isolation을 통한 이상치 제거
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from sklearn.ensemble import IsolationForest
import collections
# n_estimators : 노드 수 (50 - 100사이의 숫자면 적당하다.)
# max_samples : 샘플링 수
# contamination : 이상치 비율
# max_features : 사용하고자 하는 독립변수 수 (1이면 전부 사용)
# random_state : seed를 일정하게 유지시켜줌(if None, the random number generator is the RandomState instance used by np.random)
# n_jobs : CPU 병렬처리 유뮤(1이면 안하는 것으로 디버깅에 유리. -1을 넣으면 multilple CPU를 사용하게 되어 메모리 사용량이 급격히 늘어날 수 있다.)
clf = IsolationForest(n_estimators=100,
max_samples="auto",
contamination=0.1,
max_features=1,
bootstrap=False,
n_jobs=1,
random_state=None,
verbose=0)
# fit 함수를 이용하여, 데이터셋을 학습시킨다.
clf.fit(scale_data)
# predict 함수를 이용하여, outlier를 판별해 준다. 0과 1로 이루어진 Series형태의 데이터가 나온다.
y_pred_outliers = clf.predict(scale_data)
# 이상치의 개수를 Count하는 과정
collections.Counter(y_pred_outliers)
# 원래의 DataFrame에 붙히기. out행의 값이 -1인 것을 제거하면 이상치가 제거된 DataFrame을 얻을 수 있다.
scale_data['out']=y_pred_outliers
outliers=scale_data.loc[scale_data['out']== -1]
outlier_index=list(outliers.index)
2-2. PCA로 Isolation Forest결과 확인하기.
PCA과정을 통해 Isolation Forest의 결과를 확인하는 과정이다. PCA를 사용하기 때문에 정규화된 데이터를 사용했다.
2-2-1. RobustScaler, StandardScale를 PCA에 적용하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
scale_data_numeric = scale_data.iloc[:, range(0, len(scale_data.columns)-1)]
# 1. 정규화_Robust
from sklearn.preprocessing import RobustScaler
robust_scaler = RobustScaler()
robust_scaler.fit(sub_eda_data)
X_scaled = robust_scaler.transform(sub_eda_data)
# 2. 정규화_Standard
scaler = StandardScaler()
scaler.fit(sub_eda_data)
X_scaled = scaler.transform(sub_eda_data)
# 3. PCA(component = 3), Scaler와 무관하게 코드 동일
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
X_scaled_reduce = pca.fit_transform(X_scaled)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_zlabel("x_composite_3")
# Plot the compressed data points
ax.scatter(X_scaled_reduce[:, 0], X_scaled_reduce[:, 1], zs=X_scaled_reduce[:, 2], s=4, lw=4, label="inliers",c="green")
# Plot x's for the ground truth outliers
ax.scatter(X_scaled_reduce[outlier_index,0],X_scaled_reduce[outlier_index,1],
X_scaled_reduce[outlier_index,2],
lw=2, s=60, marker="x", c="red", label="outliers")
ax.legend()
plt.show()
# 4. PCA(component = 2), Scaler와 무관하게 코드 동일
pca = PCA(2)
pca.fit(X_scaled)
res=pd.DataFrame(pca.transform(X_scaled))
Z = np.array(res)
plt.title("IsolationForest")
b1 = plt.scatter(res[0], res[1], c='green',
s=20,label="normal points")
b1 =plt.scatter(res.iloc[outlier_index,0],res.iloc[outlier_index,1], c='green',s=20, edgecolor="red",label="predicted outliers")
plt.legend(loc="upper right")
plt.show()
RobustScaler 결과
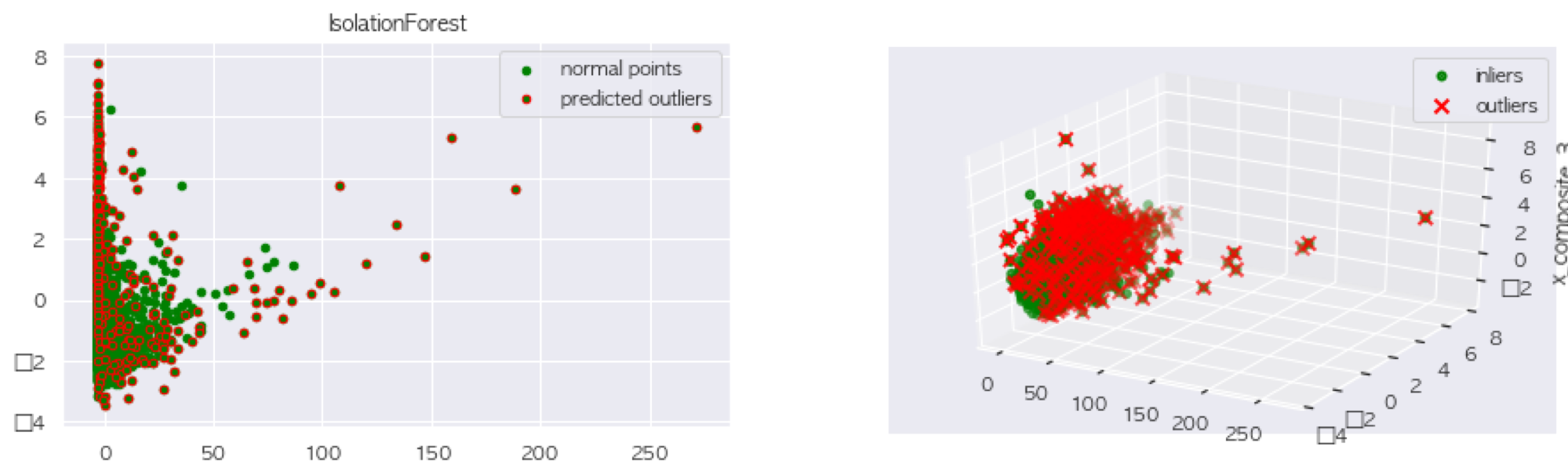
StandardScaler 결과
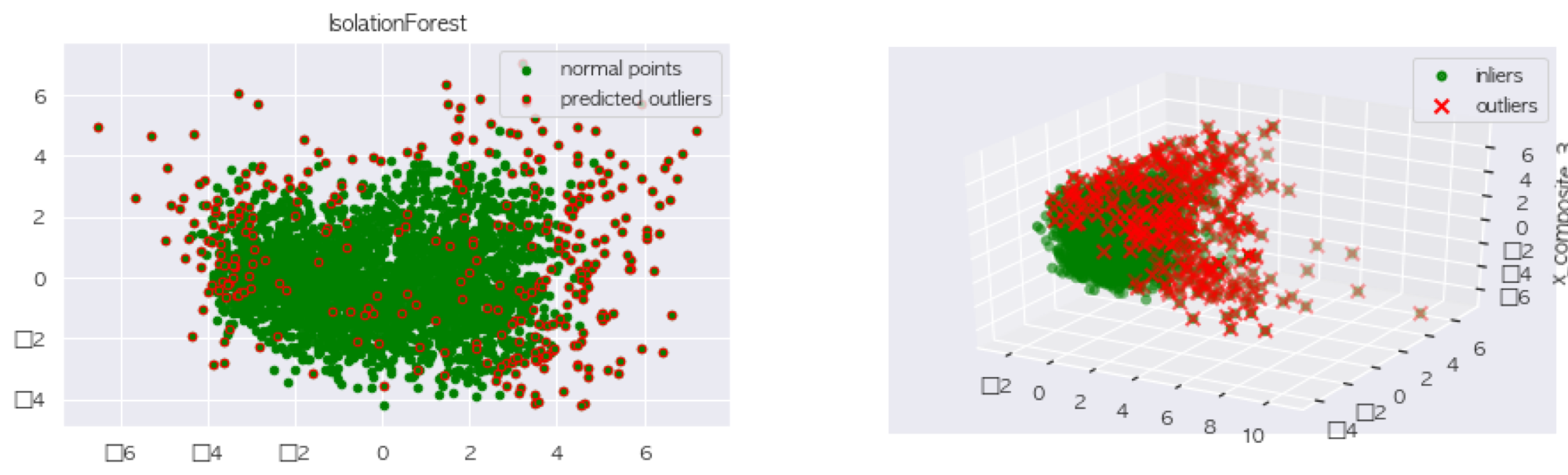
우선 동일한 데이터로 Isolation Forest를 사용했기에, 이상치는 Scaler와 무관하게 동일하다. 그러나 PCA를 진행하는 과정에서 RobustScaler를 사용했을 때, 강우량의 분산이 너무 커서 PCA결과가 한쪽으로 치우쳐져 나오는 것을 알 수 있다.
그렇기 때문에 StandardScaler를 사용한 PCA결과를 살펴보면 components가 3인 PCA에서는 이상치가 잘 보이지 않지만 component가 2인 PCA에서는 이상치 탐지가 꽤 잘 이루어진 것을 알 수 있다. 이제 이상치 탐지를 끝났으니 다음의 코드로 간단하게 이상치 제거를 할 수 있다.
1
scale_data = scale_data.loc[scale_data['out'] == 1]
이 과정을 끝으로 이상치 제거도 어느정도 끝났다. 그럼 EDA를 진행해보겠다.
3. EDA(Exploratory Data Analysis)
EDA는 탐색적 데이터 분석을 일컫는 말이다. 데이터를 분석하기 전에 그래프나 통계적인 방법으로 자료를 직관적으로 바라봄으로써 분석에 대한 통찰을 얻을 수 있다. 미세먼지는 계절성이 매우 뚜렷한 데이터이기 때문에 EDA는 꼭 필요한 과정이다.
우선 내가 사용하는 데이터셋의 형태는 다음과 같다.

3-1. 미세먼지 상태 빈도 분석
먼저 간단한 그래프를 통해 우리나라의 미세먼지 ‘매우 나쁨’, ‘나쁨’, ‘보통’, ‘좋음’의 분포를 확인해보자.
1
2
3
data['label'] = np.where(data['PM10']>150, '매우나쁨',
np.where(data['PM10']>80, '나쁨', np.where(data['PM10']>30, '보통', '좋음')))
data['year'] = data['Date'].astype(str).apply(lambda x:x[:4])
위의 코드를 사용하여 미세먼지 라벨과 년도를 데이터셋에 칼럼으로 추가하였다. 이후 matplot 라이브러리를 사용하여 간단한 파이 차트를 그려보면 다음과 같다.
1
2
3
4
5
6
7
8
f,ax=plt.subplots(1,2,figsize=(18,8))
data['label'].value_counts().plot.pie(explode=[0, 0, 0, 0.1],
autopct='%1.1f%%',ax=ax[0],shadow=False)
ax[0].set_title('Label')
ax[0].set_ylabel('Count')
sns.countplot('label', data=eda_data,ax=ax[1])
ax[1].set_title('Label')
plt.show()
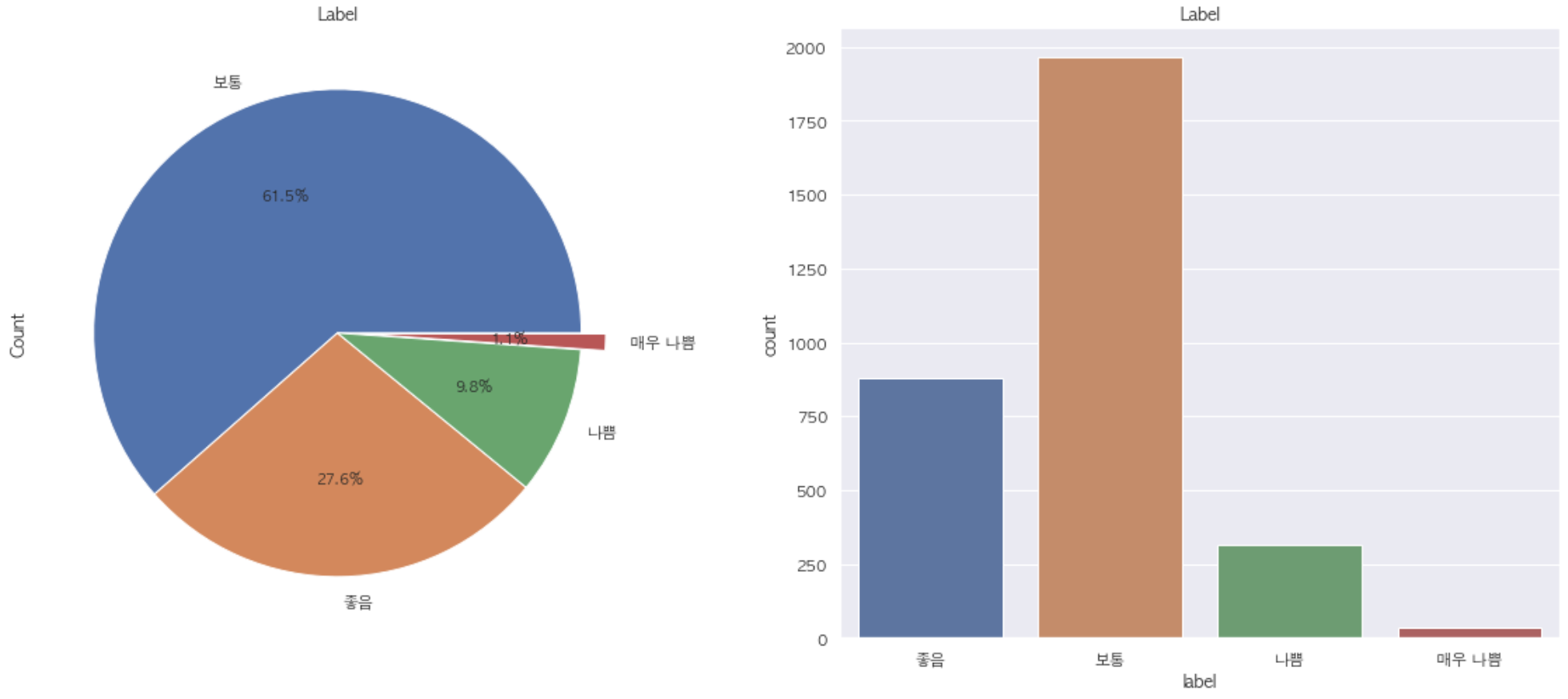
위의 그래프를 통해 약 8년간 우리나라 날씨에서 미세먼지 ‘좋음’과 ‘보통’은 전체의 89.1%를 차지하고 있음을 알 수 있다. 그러나 최근들어 미세먼지가 심해지고 있다는 느낌을 지울수가 없었다. 그래서 이를 확인해보기 위해 연도별 미세먼지 라벨링의 변화를 살펴보았다.
1
pd.crosstab(data.label,data.year,margins=True).style.background_gradient(cmap='summer_r')
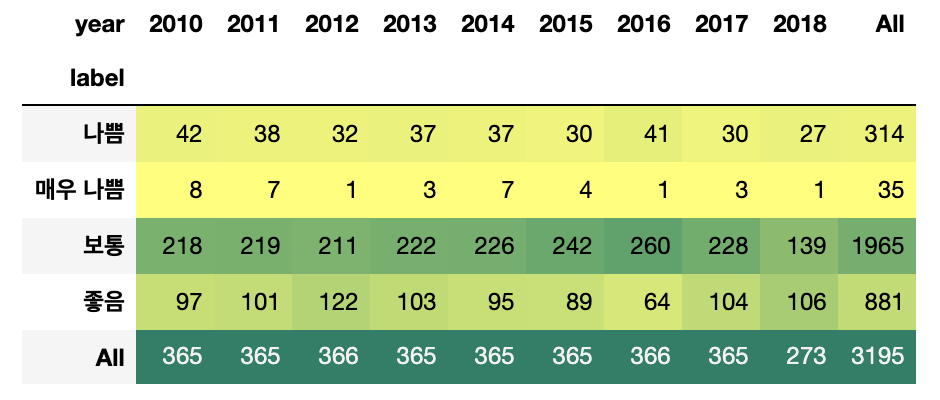
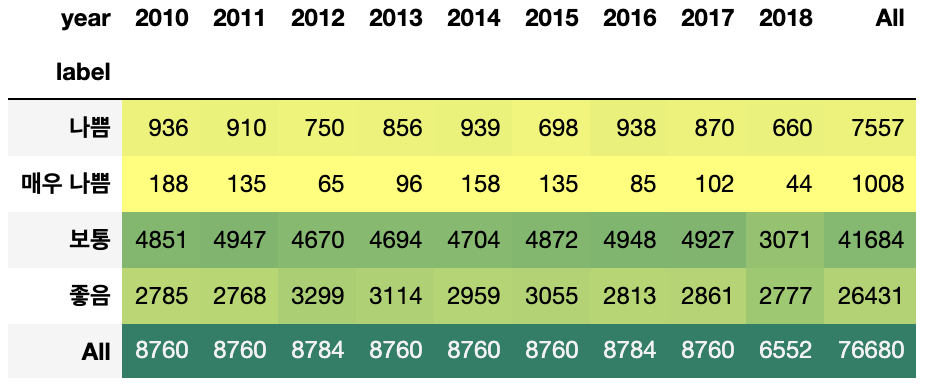
2010년부터 2018년까지 미세먼지를 일별, 그리고 시간별로 라벨링 개수를 카운팅한 결과 2016년 이후 미세먼지 ‘매우나쁨’ 일수와 시간이 늘어났다. 아마 이런 이유 때문에 사람들이 미세먼지가 과거보다 더 심해졌다는 인상을 받지 않았을까 싶다.
3-2. 상관관계 분석
다음은 변수끼리 상관계수를 살펴보자.
1
2
3
4
5
6
sns.heatmap(data.iloc[:, range(0, len(data.columns)-2)].corr(),annot=True,cmap='RdYlGn',linewidths=0.2,annot_kws={'size':20})
fig=plt.gcf()
fig.set_size_inches(18,15)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
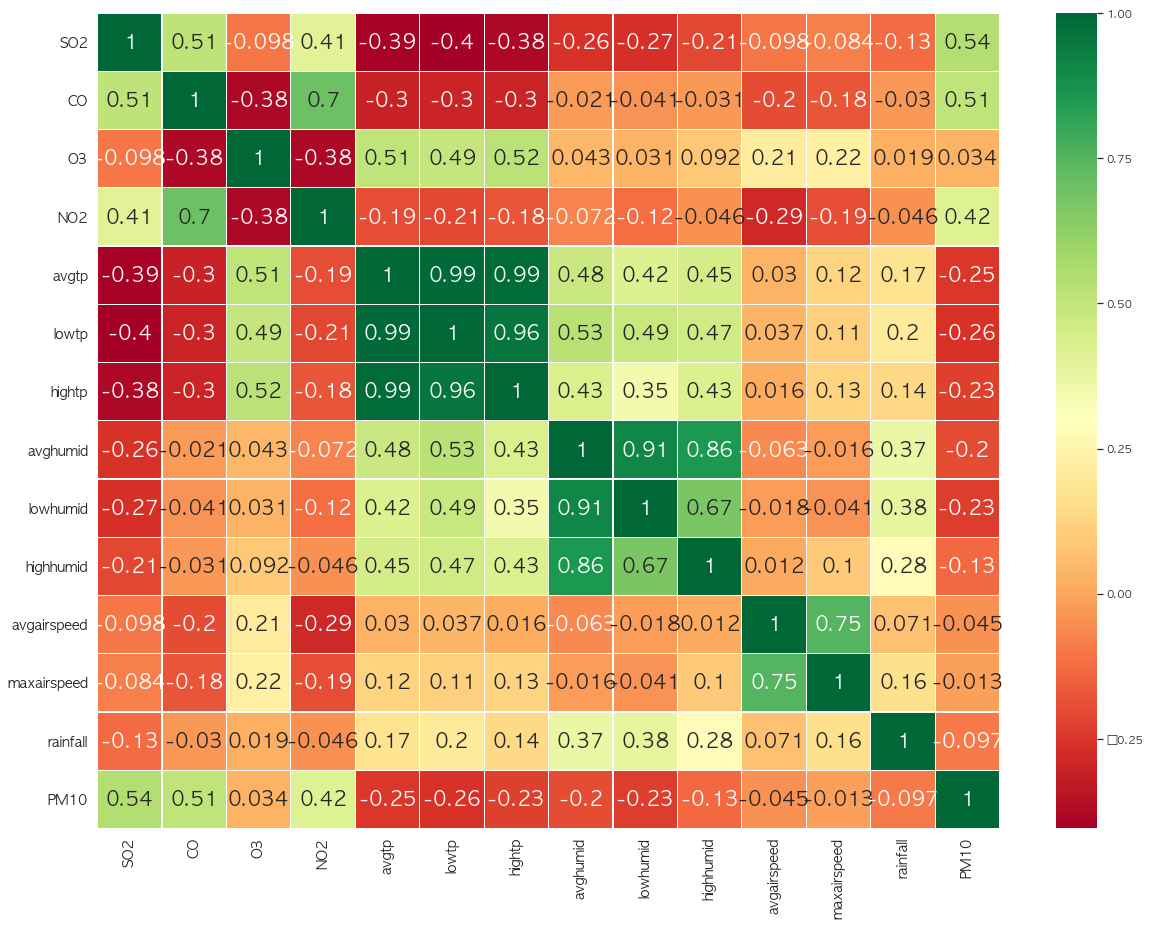
미세먼지의 전구물질로 알려져있는 SO2, CO, O3, NO2 중에서는 O3를 제외하고 나머지는 미세먼지와 확실한 양의 상관관계를 보이고 있다. 또한 기상변수 중에서는 온도변수끼리 그리고 습도변수끼리 서로 높은 상관관계를 보이고 있다. 또한 온도 및 습도와 미세먼지는 약한 음의 관계를 띄고 있어, 여름철 미세먼지가 적은 이유를 설명해주고 있다. 그러나 예상외로 풍속과 강우량은 미세먼지와의 상관관계가 낮은 것으로 결과가 나왔다.
3-3. apiriori 분석
apiriori분석은 비지도 학습에 해당하는 연관규칙 분석이다. 흔히 apiriori분석을 장바구니 분석이라고 부르기도 하는데 그 이유는 고객의 장바구니에 들어 있는 품목간의 관계를 분석한다는 의미에서 붙여졌기 때문이다.
미세먼지 EDA를 수행하는 과정에서도 apiriori분석을 수행했는데 좀 더 자세한 분석을 수행하기 위해 풍압, 지면온도 등을 추가로 제공하는 종로구 기상데이터셋을 사용했고, 연속형 숫자 데이터를 품목화 즉 범주화 시키기 위해 하루전 측정치와의 차이를 이용해 총 8단계(매우증가/약간증가/증가/다소증가/변화없음/다소감소/감소/약간감소/매우감소)로 범주화했다.
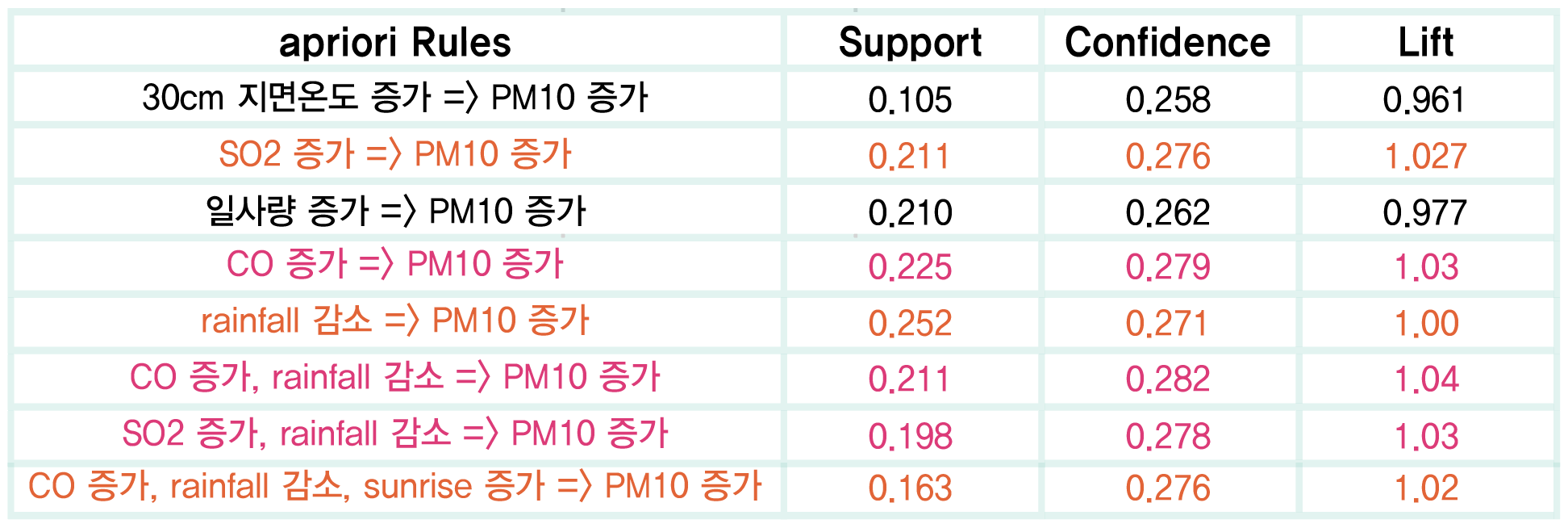
apiriori분석에서 Lift값이 1에 근접하거나 크면 유의미한 관계라고 본다. 따라서 apiriori분석에서 Lift값이 해당 조건에 만족하는 경우만 추출했는데 위와 같은 결과가 나왔다. 이를 요약하면 다음과 같다.
- 일사량이 증가하면 미세먼지가 증가한다.
- 강수량이 감소하면 미세먼지가 증가한다.
- 지면온도가 증가하면 미세먼지가 증가한다.
- CO(일산화탄소)가 증가하면 미세먼지가 증가한다.
- SO2(황산화물)가 증가하면 미세먼지가 증가한다.
위의 결과를 보면 일사량 증가와 지면온도 증가가 강수량 감소와 어느정도 상관관계를 가지고 있다고 가정하고, CO와 SO2가 미세먼지의 전구물질인 것을 감안했을때, 비교적 결과가 합리적으로 나온것 같다.
3-4. 미세먼지 전구물질 클러스터링 그래프 그리기
마지막으로 미세먼지 전구물질(SO2, CO, O3, NO2)과 미세먼지(PM10)과의 관계를 살펴보았다. 이를 위해 Clustering Graph를 그렸으며 결과는 다음과 같이 나왔다.
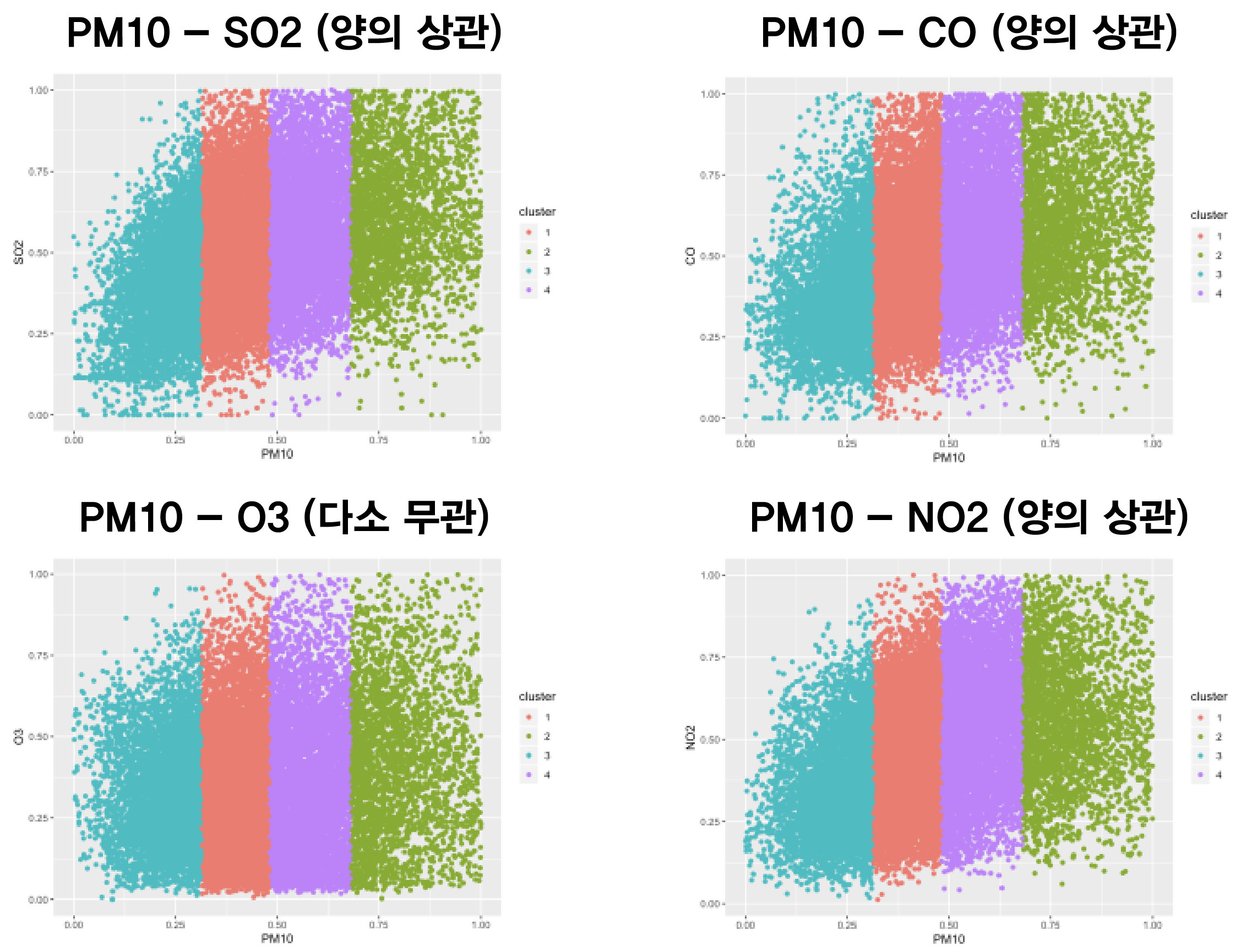
클러스터 그래프 결과 SO2, CO, NO2는 미세먼지와 비교적 뚜렷한 양의 상관관계를 가졌다. 그러나 O3는 다소 무관한 듯한 그래프 양상을 보였다.
3-5. EDA 결과 요약
이상치를 제거한 데이터셋으로 미세먼지 EDA를 진행해본 결과 우리가 흔히 알고 있는 사실과 크게 다르지 않은 결과들이 나왔다. 공장 및 자동차에서 발생되는 매연이 미세먼지와 비교적 강한 양의 상관관계를 띄었고, apiriori 분석을 통해 날씨 변수와의 미세먼지 EDA서도 강수량과 미세먼지의 반비례 관계를 확인했다. 이제 EDA까지 마무리 했으니 본격적으로 미세먼지 예측 모델을 만들어야 한다. 다음 포스팅에서 이어서 글을 쓰겠다.
reference
- 서울시 공원일몰제 시행에 대비한 수직빌딩숲 입지 선정 및 제안 (김민기, 유민형, 2018)
- donghwa-kim.github.io_Isolation Forest
- ko.logpresso.com
- datascienceschool.net