개인적인 호기심에서 진행한 연구입니다. 제가 잘못 알고 있는 점이나 수정•보완이 필요한 부분은 댓글로 알려주시면 감사드리겠습니다. 그럼 시작하겠습니다.
들어가는 글
앞선 포스팅인 ‘2편’에서 미세먼지 데이터셋의 간단한 EDA와 Outlier(이상치)제거를 진행했다. 이후 이상치가 제거된 데이터를 가지고 추가적인 분석을 진행해보았다.
1. Feature Selection
13차원의 독립변수 데이터셋은 사실 그리 엄청 큰 차원을 가진 데이터셋은 아니다. 그러나 차원의 크기가 매우 크지 않아도 Feature Selection을 통해 얻을 수 있는 장점들은 다양하다. 이 장점들에 대해 잠깐 살펴보고 가도록 하겠다.

1-1. Overfitting
Overfitting은 Machine Learning, Deep Learning 모델을 구현할 때 가장 사용자를 혼란스럽고 어렵게 하는 문제 중 하나이다. Overfitting을 간단히 설명하자면, 말 그대로 너무 과도하게 학습 데이터에 대해 모델을 Learning하여, 모델이 학습 데이터 이외의 데이터에선 성능을 제대로 발휘하지 못하는 것을 말한다. 따라서 Overfitting을 제대로 관리하지 못하면 실전에서는 활용할 수 없는 데이터 모델이 되기 때문에 Overfitting을 관리하는 것은 매우 중요한 일임을 알 수 있다.
이때 Reguralization과 Feature Selection을 적절히 사용하면 Overfitting을 예방할 수 있다. 이는 데이터 셋 내에서 불필요한 상관관계가 있는 변수들을 줄여주고, 모델이 원할하게 학습 데이터 내에서 일반적인 패턴을 발견할 수 있게 도와준다.
1-2. 차원의 저주(Curse of Dimensionality)
1차원의 데이터셋과 10,000차원의 데이터셋을 분석하는 것은 매우 다를 것이다. 일반적인 생각으로는 차원이 많으면 종속변수를 고려하기 위한 독립변수들이 많아져서 성능이 증가할 것이라고 생각한다. 그러나 어디까지나 이런 가정은 데이터가 비교적 충분할 경우에만 성립한다.
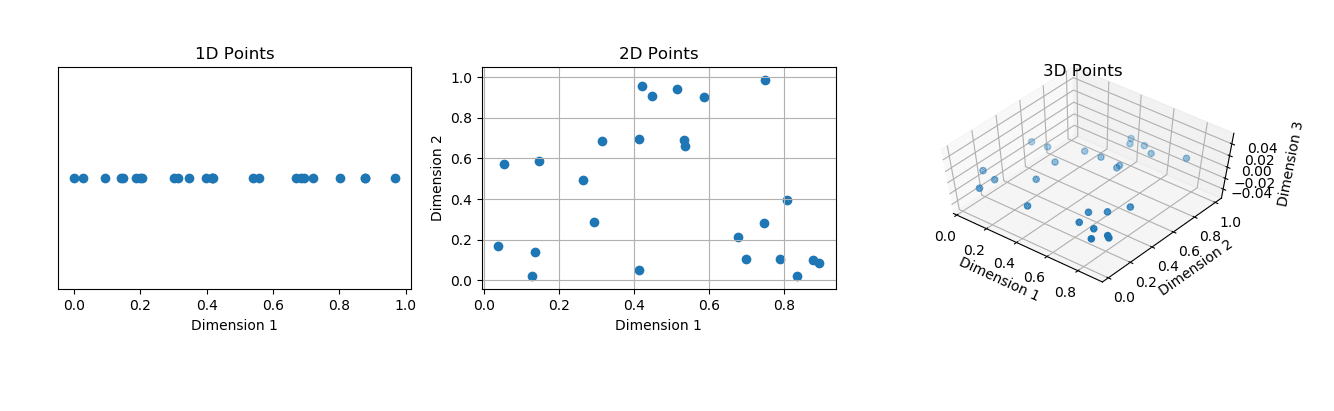
위의 이미지를 보자. 각 차원에 들어있는 데이터의 양은 보다시피 일정함을 알 수 있다. 그러나 차원이 늘어나면 늘어날수록 차원에 할당되는 부피 혹은 넓이는 기하급수적으로 커진다. 그렇기에 데이터의 양이 일정하다면 차원이 증가할수록 데이터의 밀도가 떨어진다. 따라서 차원의 저주를 막기 위해서는 기하급수적으로 증가하는 차원의 부피만큼 데이터의 양도 기하급수적으로 늘려줘야한다.
그러나 데이터 양을 기하급수적으로 늘리는 것은 Computing Time과 경제적인 관점에서 큰 부담이다. 이런 이유로 모델을 만들 때 가능한 데이터의 차원을 낮춰서 분석을 진행하는 것이 좋다. 이외에도 Feature Selection을 통한 변수 추출의 장점을 정리하면 다음과 같다.
-
- Overfitting의 위험성 감소
-
- 차원의 저주 예방
-
- Computing Time 감소
-
- 결과 해석의 편의성 증가
-
- 모델의 성능 향상
따라서 지금부터 13개 변수를 전부 사용해서 모델을 만드는 것이 아닌, 일부 변수만 사용해서 모델을 만들겠다. 어떤 변수를 선택하는것이 좋을까?
2. 어떤 변수를 가지고 미세먼지 예측을 진행해야 할까?
본격적으로 변수 선택을 진행해보겠다. 우선 본 연구의 목적은 수직빌딩숲이 얼마나 미세먼지를 줄여줄 수 있는가?로 수직빌딩숲이 가져오는 효과를 입증할 수 있을만한 변수를 선택해야했다.
그렇다면 수직빌딩숲이 가져오는 효과란 무엇인가? 수직빌딩숲은 일반적인 건물보다 면적대비 식재량이 많다. 따라서 수직빌딩숲의 효과라함은 많은 식물과 나무로부터 얻는 효과일 것이다.
식물과 나무는 지면 온도를 낮춰주는것과 같이 기상에 관련한 여러 긍정적인 효과들이 있지만, 수직빌딩숲 하나로 기상에 영향을 미치기란 현실적으로 어렵다고 생각했다. 그래서 보다 미시적인 Scale로 들어가 나무 한 그루의 효과에 집중해서 변수를 선택하고자 했다.
2-1. 방배동 소라어린이공원의 수직빌딩숲에 심어질 식재 수
수직빌딩숲의 효과를 알아보기 위해 방배동 소라어린이공원에 수직빌딩숲이 지어진다고 가정하고 분석을 진행했다. 분석을 위해 기본적인 가정을 먼저 설정하고 가겠다.
| 보스코 베르티칼레 | 소라 수직빌딩숲(가상) | |
|---|---|---|
| 소재지 | 이탈리아 밀라노 | 서울 방배동 |
| 높이 | 약 186m | 약 100m |
| 면적 | 총 758.37\(m^2\) | 총 1,200\(m^2\) |
| 작은나무 | 480그루 | 403그루 |
| 중간 크기 나무 | 300그루 | 252그루 |
| 피복식물 | 15,000개 | 12,600개 |
| 관목 | 4,500개 | 3,780개 |
방배동 소라어린이공원의 사유지는 약 1,200\(m^2\)로 추정된다. 따라서 이 면적 전체에 수직빌딩숲이 지어진다는 가정하에 면적을 설정했고, 서울의 초고층 빌딩의 마지노선인 49층 아파트가 199m, 주변 아파트의 층고를 고려해 높이는 100m로 설정했다.
이렇게 정해진 높이와 면적을 기준으로 보스코 베르티칼레와 소라 수직빌딩숲의 부피비를 계산한 결과 다음의 부피비가 나왔다.
\[소라 \, 수직빌딩숲 : 보스코 \, 베르티칼레 = 0.84 : 1\]따라서 보스코 베르티칼레의 식재 수에 0.84를 곱해 소라 수직빌딩숲의 최종 식재량을 결정하였다. 또한 식재의 수를 \(m^2\)으로 환산한 결과 소라 수직빌딩숲의 \(m^2\)당 나무 수는 0.14그루이다.
2-2. 나무의 전구물질 정화 효과
\(m^2\)당 나무 수를 구했으니 나무 한 그루당 전구물질 정화 효과에 대해 조사해보았다. 미국 National Recreation and Park Association의 David J.NOWAK에 따르면 나무 한 그루당 대기유해물질 감소량은 다음과 같다.
| 유해물질 명 | 감소량 |
|---|---|
| Particulate Matter | 13%\(m^2\) |
| Ozone | 16%\(m^2\) |
| Sulfor dioxide | 16%\(m^2\) |
| Nitrogen dioxide | 8%\(m^2\) |
| Carbon monoxide | 0.05%\(m^2\) |
위 자료에 입각해 미세먼지 예측 모델 변수를 SO2, NO2, CO, O3로 설정한 후, 미세먼지 예측 모델을 설계해보겠다.
3. LSTM을 통한 미세먼지 절감 예측
3-1. 데이터셋 분할
우선 위 자료를 이용하기 위해 다음과 같은 타임라인으로 train 데이터와 test 데이터를 구분했다. 그리고 test 데이터에는 추가로 식재에 의한 전구물질 감소의 효과를 가정했다.

위의 Timeline에서도 볼 수 있듯이 Test Data에는 이미 수직빌딩숲이 18.03.01자로 완공되었다는걸 전제로 분석을 수행했다. 따라서 Test Data의 독립변수들에는 나무의 절감 효과를 인위적으로 적용시켜주었다.
3-2. LSTM 선정 이유
수직빌딩숲 효과를 입증하기 위한 미세먼지 예측 모델 구축을 위해 본 연구에서 채택한 알고리즘은 LSTM이다. LSTM은 전통적인 시계열 분석 딥러닝 알고리즘은 RNN에서 Learning Time과 Vanishing Gradient 문제를 개선한 알고리즘으로 시계열 분석에 뛰어난 성능을 보인다고 알려져있는 딥러닝 알고리즘이다. LSTM 구현 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def lstm_cell():
cell = tf.nn.rnn_cell.LSTMCell(num_units=rnn_cell_hidden_dim,
forget_bias=forget_bias, state_is_tuple=True, activation=tf.nn.softsign)
if keep_prob < 1.0:
cell = tf.contrib.rnn.DropoutWrapper(cell, output_keep_prob=keep_prob)
return cell
stackedRNNs = [lstm_cell() for _ in range(num_stacked_layers)]
multi_cells = tf.contrib.rnn.MultiRNNCell(stackedRNNs, state_is_tuple=True) if num_stacked_layers > 1 else lstm_cell()
hypothesis, _states = tf.nn.dynamic_rnn(multi_cells, X, dtype=tf.float32)
print("hypothesis: ", hypothesis)
hypothesis = tf.contrib.layers.fully_connected(hypothesis[:, -1], output_data_column_cnt, activation_fn=tf.identity)
loss = tf.reduce_sum(tf.square(hypothesis - Y))
# optimizer = tf.train.RMSPropOptimizer(learning_rate) # LSTM과 궁합 별로임
optimizer = tf.train.AdamOptimizer(learning_rate)
train = optimizer.minimize(loss)
# RMSE(Root Mean Square Error)
rmse = tf.sqrt(tf.reduce_mean(tf.squared_difference(targets, predictions)))
print('학습을 시작합니다...')
for epoch in range(epoch_num):
_, _loss = sess.run([train, loss], feed_dict={X: trainX, Y: trainY})
if ((epoch+1) % 100 == 0) or (epoch == epoch_num-1): # 100번째마다 또는 마지막 epoch인 경우
# 학습용데이터로 rmse오차를 구한다
train_predict = sess.run(hypothesis, feed_dict={X: trainX})
train_error = sess.run(rmse, feed_dict={targets: trainY, predictions: train_predict})
train_error_summary.append(train_error)
# 테스트용데이터로 rmse오차를 구한다
test_predict = sess.run(hypothesis, feed_dict={X: testX})
test_error = sess.run(rmse, feed_dict={targets: testY, predictions: test_predict})
test_error_summary.append(test_error)
corrects = tf.equal(test_predict, testY)
accuracy = tf.reduce_mean(tf.cast(corrects, dtype = tf.float64))
# 현재 오류를 출력한다
print("epoch: {}, train_error(A): {}, test_error(B): {}, B-A: {}, accuracy: {}".format(epoch+1, train_error, test_error, test_error-train_error, accuracy))
3-3. LSTM 모델 결과
그렇다면 LSTM 예측 모델의 결과는 어떨까?
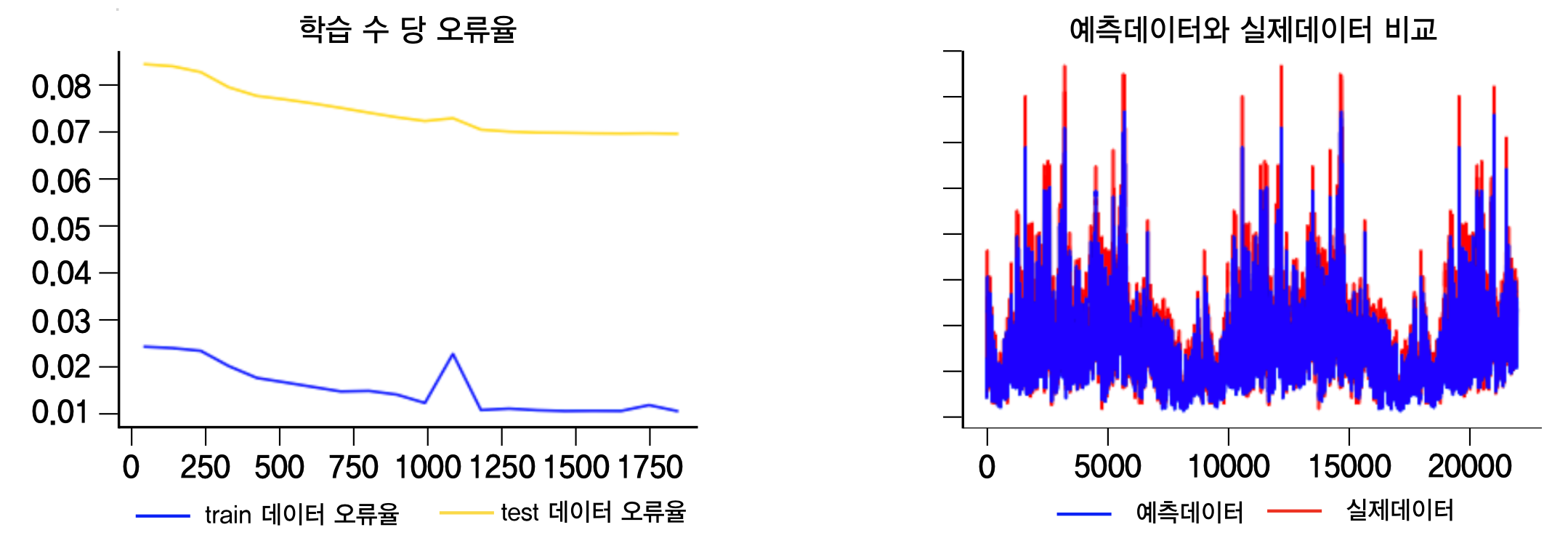
LSTM 예측 모델 결과 2000번의 학습을 거듭하면서 최종 Test Data의 RMSE는 0.0701정도가 나왔으며, 오른쪽 그래프를 보더라도 LSTM 모델이 미세먼지 경향을 잘 반영한다는 것을 알 수 있다. 이제 모델 생성은 끝났으니 이 모델을 이용하여 수직빌딩숲의 효과를 입증해보도록 하자.
4. 수직빌딩숲 효과 검증
이제 Test Data(위 그래프의 test data가 아닌 타임라인의 test data)에서 나무 한 그루당 대기오염물질 정화량을 적용한 다음에 수직빌딩숲의 효과를 살펴보자.
1
2
3
4
5
6
7
8
9
#제일 앞의 24일은 빠지고 예측이 되는거
dataZ = []
for i in range(0, len(y_test)-1):
recent_data = np.array([x_test[i : i+24]])
test_predict = sess.run(hypothesis, feed_dict={X: recent_data})
print("test_predict", test_predict[0]*(1-0.13))
finedust = reverse_min_max_scaling(fine_dust_test,test_predict[0]*(1-0.13))
print("fine_dust", finedust[0])
dataZ.append(finedust[0])
위의 코드를 통해 모델에 대기오염 정화 효과를 적용한 2018.03.01 ~ 2018.04.30 데이터를 넣어서 예측을 진행했다
test_predict[0]*(1-0.13)에서 (1-0.13)를 곱해주는 이유는 나무 한 그루당 미세먼지 절감량이 13%\(m^2\)이기 때문이다. 따라서 전구물질로 인한 절감량과 미세먼지 직접 절감량을 동시에 고려해주기 위해 이와 같은 곱셈을 추가해주었다.
4-1. 수직빌딩숲 효과
수직빌딩숲의 효과은 어떤 효과가 있었을까? 먼저 수직빌딩숲에 의해 평균 미세먼지 저감량이 시간당 \(m^2\)당 2.41정도였다. 매우 미약한 수치로 보이겠지만 소라 수직빌딩숲 전체 면적으로 따지면 시간당 289,200의 감소 효과를 볼 수 있다.
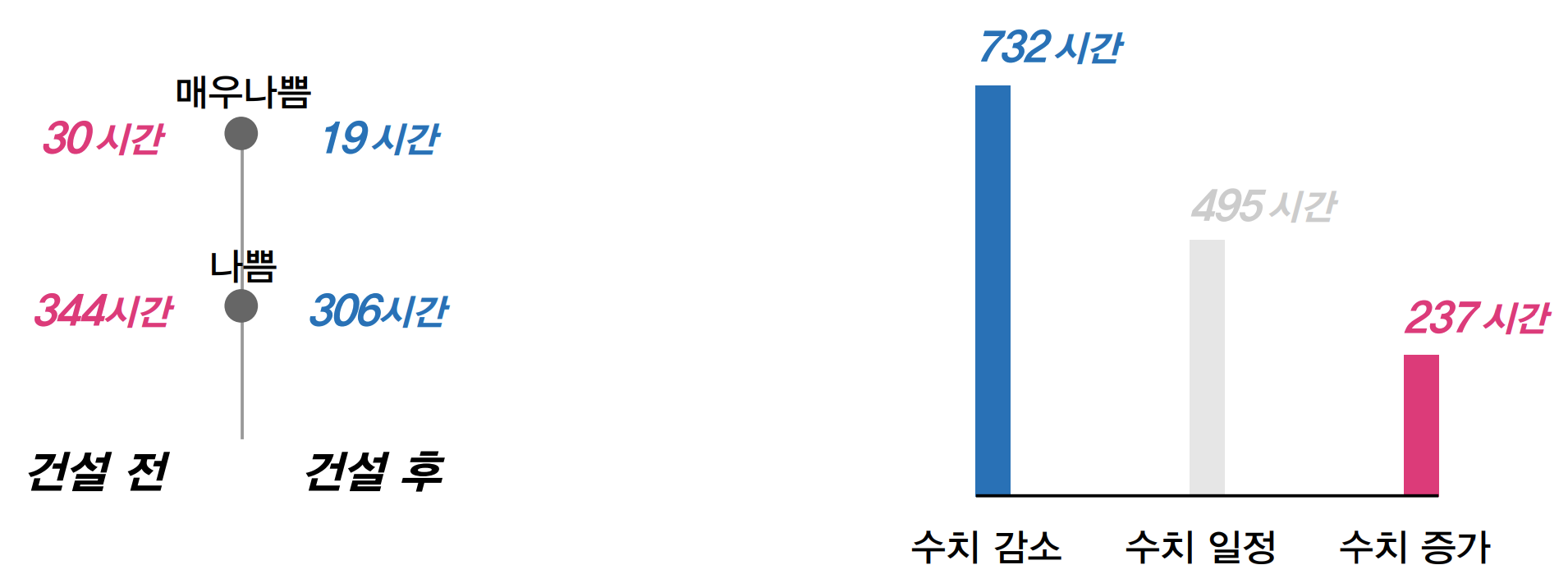
미세먼지 감소를 자세히 살펴보면 다음과 같다. 먼저 건설 후에 건설 전보다 매우나쁨이 11시간 줄었다. 또한 나쁨 역시 38시간 줄었다. 또한 총 1,465시간 중에서 거의 절반인 732시간에서 수치가 감소했다. 따라서 수직빌딩숲이 실제로 미세먼지를 저감하는데에 도움이 된다고 할 수 있다.
4-1-1. Envimet
여기에 더뷸어 소라 수직빌딩숲이 들어서면 그 일대로 빌딩품이 불 것이다. 따라서 빌딩풍의 양상을 파악하기 위해 총 6가지의 경우의 수를 가지고 Envimet을 활용해 바람시뮬레이션을 진행했다. 서울은 주로 서풍이 불기 때문에 바람시뮬레이션을 돌릴때 서풍으로 풍향을 맞춰놓고 진행했다.
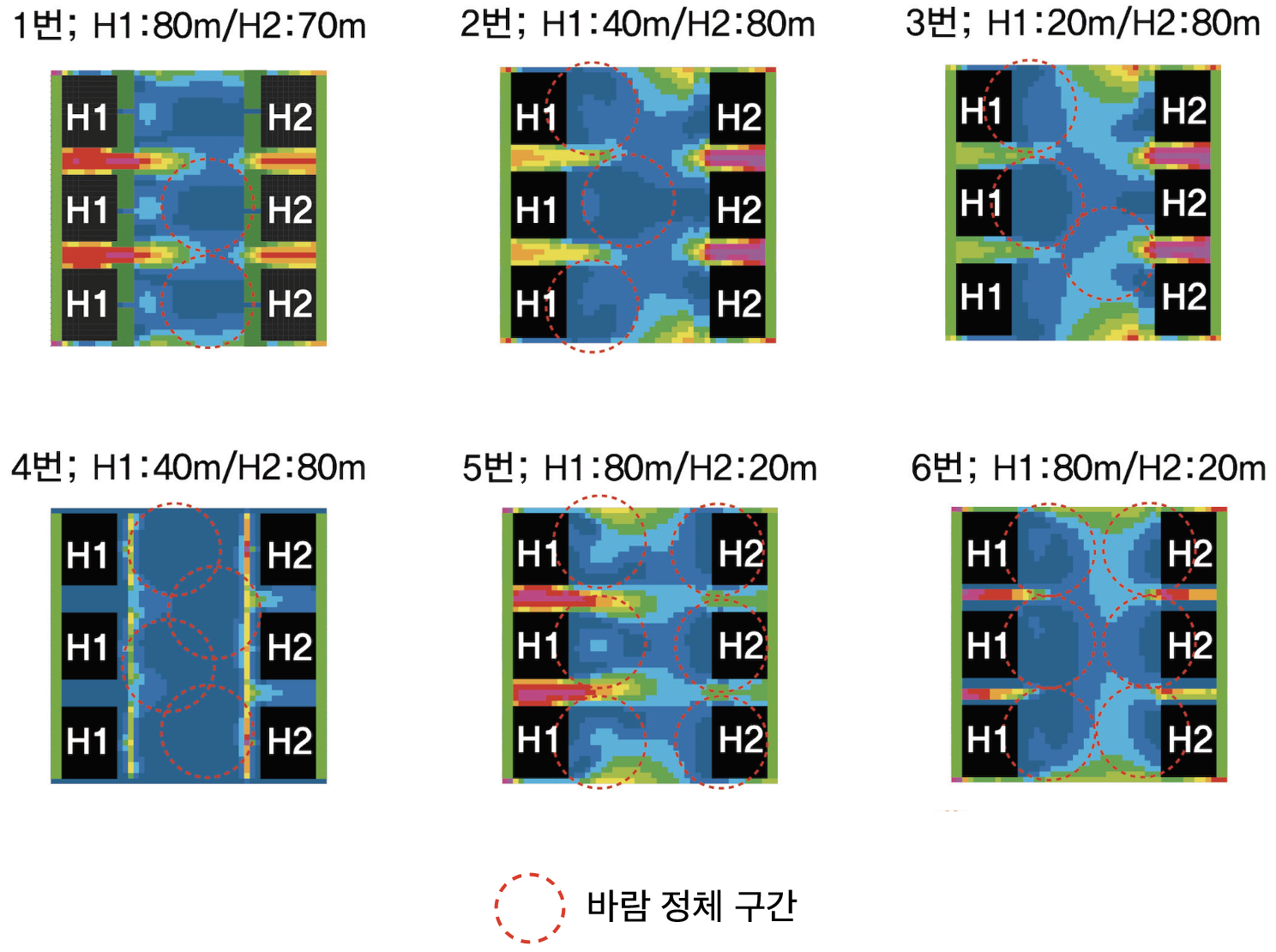
위의 그림에서 볼 수 있듯이 6가지 경우 모두에서 빌딩 근처에 바람 정체 구간이 생기는 것을 볼 수 있다. 따라서 만약 소라 수직빌딩숲이 생긴다면 건물 주위로 바람이 정체되고, 정체된 바람 속에 있는 미세먼지의 감소량은 단순히 LSTM으로 예측한 결과보다 더 클 것으로 예상된다.
5. 칼럼을 마치면서.

위의 기사는 2020년 11월 06일에 한국경제에서 발행된 기사를 캡쳐한 사진이다. 헤드라인과 기사를 보면 한국경제는 서울시가 공원 매입에 4000억이나 빚을 내는 것에 다소 부정적인 입장을 취하고 있다. 그러나 공원일몰제에 대해 한번쯤은 깊게 알아보거나, 이 시리즈를 다 보신 분들이라면 빚을 내서라도 공원을 매입하는 서울시의 입장이 어느정도 이해가 되리라고 개인적으로 생각해본다.
빠르게 산업화를 진행한 우리나라의 역사 속에서 공원은 언제나 후순위에 놓여져 있었다. 그리고 여러 사람들이 공원의 중요성을 너무나도 잘 알고 있지만, 막상 이런 이슈가 나오면 언제 그랬냐는듯 공원을 마치 ‘아픈 손가락’ 취급한다. 그러나 공원은 항만, 철도, 공항에 뒤지지 않을 정도로 우리의 삶에서 매우 중요한 요소이다.
그렇기에 이 칼럼을 통해 우리가 소중하게 생각하는 공원이 현재 사라질 위기에 쳐해있고, 자금 마련으로 어려움을 겪고 있는 서울시에게 내가 할 수 있는 방법으로 도움을 주고 싶었다. 도움을 주는 방법으로 데이터 분석을 사용해 최대한 결과의 신빙성을 확보하는데 주력했고, 이런 노력이 글을 읽는 사람에게 부디 와다았기를 바래본다.
마지막으로 서울시와 정부, 공원을 지키고자 하는 모든 사람들의 노력으로 공원일몰제 이슈가 널리널리 퍼졌으면 좋겠다. 그래서 지주와의 대립 및 갈등이 아닌 원만한 합의로 이 사안을 해결할 수 있게 모두의 지혜가 모이기를 바란다. 더이상 공원이 ‘아픈 손가락’ 취급을 안 받을 수 있게 우리 모두 조금씩 그리고 지속적으로 이 문제에 관심을 가지질 바라면서 글을 끝마친다.
reference
- 서울시 공원일몰제 시행에 대비한 수직빌딩숲 입지 선정 및 제안 (김민기, 유민형, 2018)
- donghwa-kim.github.io_Isolation Forest
- ko.logpresso.com
- datascienceschool.net