잘못된 내용은 언제든지 밑의 댓글로 알려주세요!
Linear Regression
Linear Regression, 선형 회귀는 회귀 분석의 가장 기본적인 형태로써 종속 변수 Y와 한 개 이상의 독립 변수인 X의 관계를 가장 잘 예측할 수 있는 회귀선을 찾는 것을 목표로 하고 있습니다.
| linear regeression graph | linear regression 공식 |
|---|---|
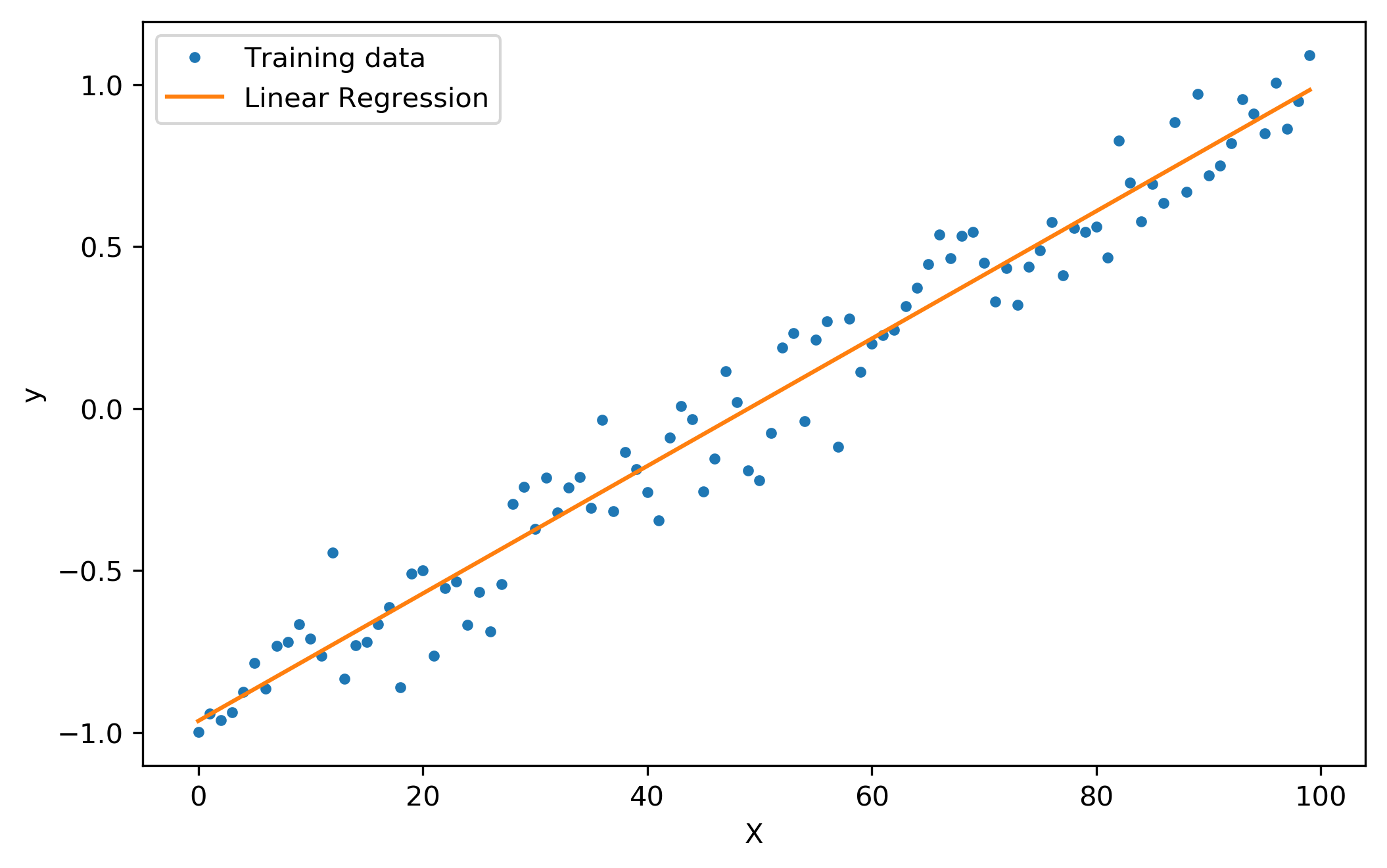 |
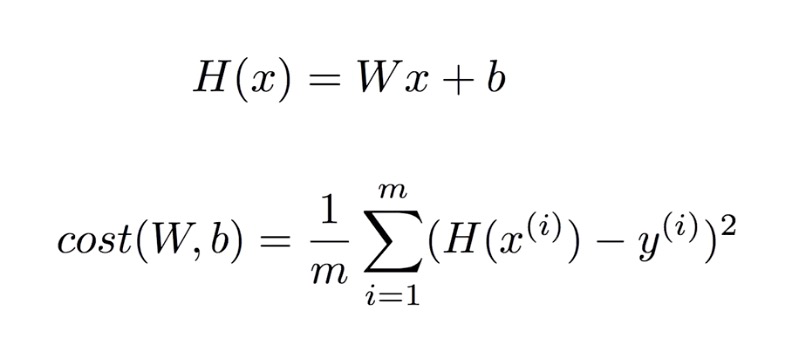 |
따라서 Regression을 통해 Cost 함수를 작게 만드는 W와 b를 구하는 것이 목표이고, 이를 위해서는 H(x)와 Y의 차이를 최소로 하는 W, b를 구해야 합니다. 이 과정을 tensorflow로 구현해보겠습니다.
1. tensorflow import
1
2
3
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import matplotlib.pyplot as plt
먼저 텐서플로우와 그래프를 그리기 위한 matplot 라이브러리를 import 해줍니다. 여기서 주의해야할 점은 tensorflow 2.0으로 바뀌게 되면서 import tensorflow as tf로 tensorflow를 import하면
tensorflow의 placeholder 명령어를 사용할 수 없습니다. 그렇기에 위의 코드처럼 tensorflow를 import 해주는 것에 주의하세요.
2. 변수 및 H(x)값 설정
1
2
3
4
5
6
7
8
# X, Y : 변수
X = tf.placeholder(tf.float32, shape=[None])
Y = tf.placeholder(tf.float32, shape=[None])
# W, b : Cost 값
W = tf.Variable(tf.random_normal([1]), name = 'weight')
b = tf.Variable(tf.random_normal([1]), name = 'bias')
# H(x) : linear formula
hypothesis = X*W + b
여기서는 X•Y, W•b 변수의 차이점을 주목해야 합니다. X와 Y는 독립변수와 종속변수로써 일정 값이 들어갈 변수이기 때문에 tf.placeholder로 지정해주었습니다. 반면에 W, b는 regression을 위해
구해야할 변수입니다. 따라서 tf.placeholder대신 tf.Variable로 변수를 설정하였습니다.
3. Cost 함수 지정
1
2
cost = tf.reduce_mean(tf.square(hypothesis - Y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01)
cost 함수는 선형회귀 분석에서 실제값과 회귀값의 차이인 ‘거리’를 제곱해주는 함수로 이를 tf.reduce_mean을 이용해 함수를 선언해줍니다. 이제 중요한 함수인 tf.train.GradientDescentOptimizer를 살펴보기 위해 Gradient Descent가 무엇인지 살펴보겠습니다.
3-1. Gradient Descent
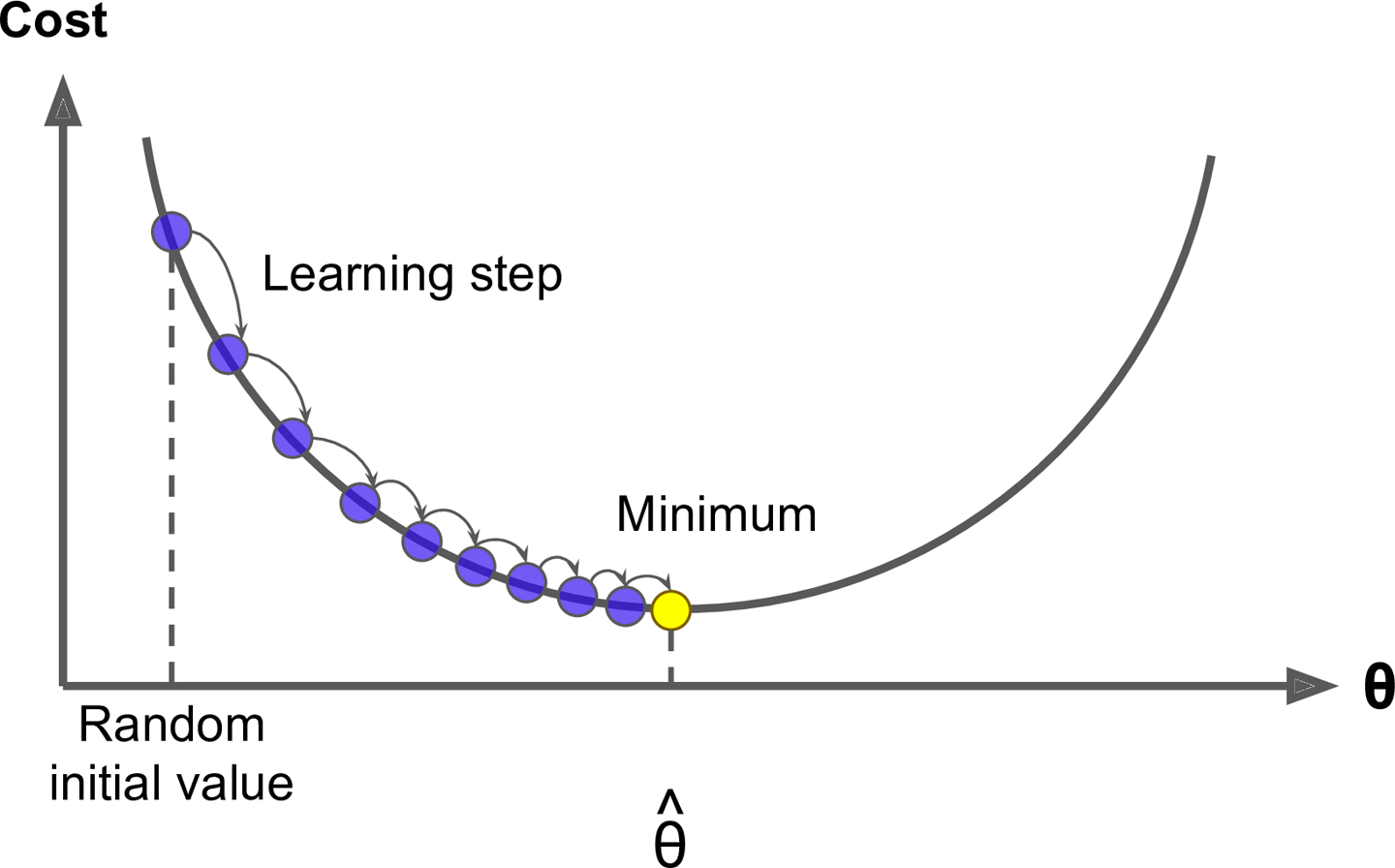
처음에도 말했듯이 선형 회귀의 목적은 Cost 값을 최소로 만드는 W, b를 찾는 것입니다. 그리고 많은 종류의 머신러닝, 딥러닝 모델에서 해당 과정을 통해 흔히 경사하강법, Gradient Descent를 사용합니다. 경사하강법 설명을 위해
tf.train.GradientDescentOptimizer를 파이썬 코드로 풀어서 같이 보도록 하겠습니다.
1
2
3
4
learning_rate = 0.01
gradient = tf.reduce_mean((W*X - Y) - X)
descent = W - learning_rate*gradient
update = W.assign(descent)
우선 쉬운것부터 설명하는게 좋을 것 같습니다. learning_rate는 위 그래프의 learning_step이랑 같은 의미로 ‘학습 간격’이라고 보시면 됩니다. 즉, learning_rate가 커지면 더 빠르게 학습하는 것이고, 작으면 더 촘촘히 학습을 진행하는 것입니다.
이 말만 보면 많은 분들이 ‘learning_rate가 크면 훨씬 좋겠네!!’ 라고 오해하실 수 있기에 그림 하나를 보여주고 넘어가겠습니다.
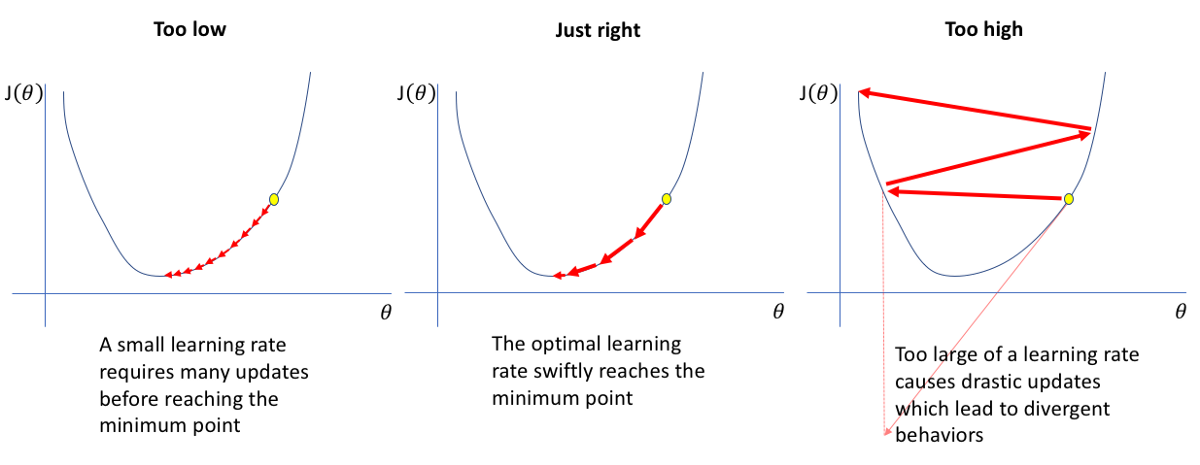
위 그림에서 보시는 것처럼 cost 함수가 ‘convex function’과 같은 그래프가 아니라면 learning_rate를 무조건 늘렸다가는 cost 함수의 최저점을 건너뛸 수 있습니다. 그렇기에 learning_rate는 작은 수를 시작으로 조금씩 조정해가며 모델을 만들어야 합니다.
이제 위 코드에서 가장 중요한 gradient를 설명해드리겠습니다. 많은 딥러닝, 머신러닝 모델들이 최저인 cost를 찾기 위해 ‘미분’을 이용합니다. 그 이유는 고등학교 수학시간에서 배웠듯이 최저점일수록 함수의 기울기가
0이 될 확률이 높기 때문입니다. 자 그럼 이제 cost 함수를 미분해보겠습니다.
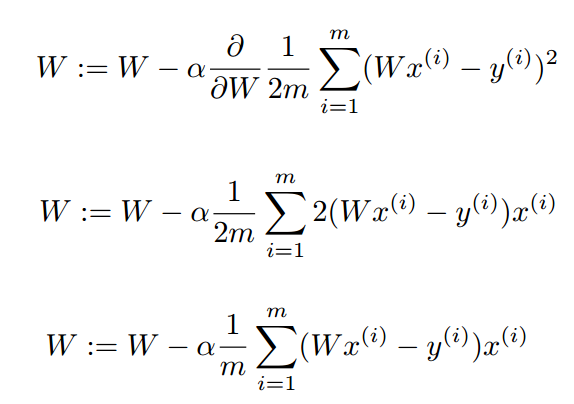
위의 사진은 cost함수 미분 과정을 차례대로 보여드린 것입니다. 눈썰미가 있으신 분들은 알아보셨겠지만 위 코드의 gradient는 밑의 미분 값을 의미하는 코드임을 알 수 있습니다.
이제 설명은 끝났습니다. 이를 요약하자면 tf.train.GradientDescentOptimizer는 cost 함수를 미분한 후 cost 함수의 기울기만큼 W를 움직여 기울기가 0에 가까운 점을 찾는 함수라고 할 수 있습니다.
4. 결과 및 그래프
이제 gradiendt descent 함수까지 만들었으니 이를 모델에 적용하여 학습시켜보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
train = optimizer.minimize(cost)
# 그래프를 위해 빈 리스트를 생성하였습니다. 필수는 아닙니다.
W_list = [ ]
b_list = [ ]
cost_list = [ ]
step_list = [ ]
# 2000번 반복학습
for step in range(2001):
cost_val, W_val, b_val, _ = sess.run([cost, W, b, train],
feed_dict = {X:[1, 2, 3, 4, 5],
Y:[2.1, 3.1, 4.1, 5.1, 6.1]})
if step%20 == 0:
step_list.append(step)
W_list.append(W_val)
cost_list.append(cost_val)
b_list.append(b_val)
print(step, cost_val, W_val, b_val)
이제 학습이 끝났으므로 결과는 그래프를 통해 살펴보겠습니다.
1
2
3
4
5
plt.plot(step_list, W_list)
plt.show()
plt.plot(step_list, b_list)
plt.show()
| Step W graph | Step b graph |
|---|---|
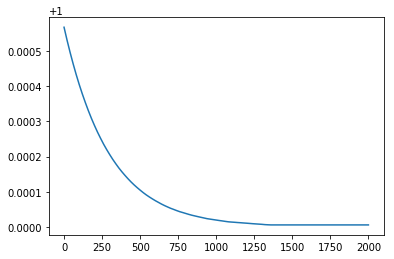 |
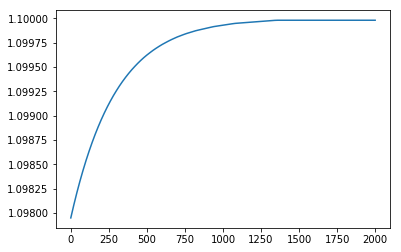 |
학습이 진행될 때마다 W는 1로 b는 1.1로 수렴하는 것을 보아 성공적으로 tensorflow가 linear regression을 수행했음을 알 수 있습니다.
1
2
plt.plot(step_list, cost_list)
plt.show()
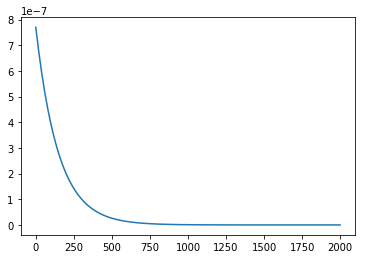
또한 cost 값 역시 학습이 진행될 수록 0으로 수렴하고 있는 것을 보실 수 있습니다. 이해에 도움이 되셨길 바라면서 전체 코드를 끝으로 글을 마무리 하겠습니다.
5. 전체 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# import tensorflow as tf
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import matplotlib.pyplot as plt
# X, Y의 값에 따라 W, b가 바뀌는 것이므로
# X, y는 변수보다는 placeholder로 선언해주는 것이 좋다.
X = tf.placeholder(tf.float32, shape=[None])
Y = tf.placeholder(tf.float32, shape=[None])
# 우리가 원하는 것은 가중치(W)와 상수(b)를 찾는 것.
# W와 b는 여기서 상수이므로 placeholder대신 Variable로 선언해주는 것이 좋다.
# 어차피 뒤에서 global_variables_initializer을 통해 초기화 된다.
W = tf.Variable(tf.random_normal([1]), name = 'weight')
b = tf.Variable(tf.random_normal([1]), name = 'bias')
hypothesis = X*W + b
# cost 함수를 구하는 공식
cost = tf.reduce_mean(tf.square(hypothesis - Y))
# Linear Regression의 목적은 cost를 최소화 하는 것.
# GradientDescent의 주체는 Cost이다.
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01)
train = optimizer.minimize(cost)
# tensorflow는 run을 하기 전에 항상 tf.Session을 실행시켜주어야 한다.
# 그리고 tf.global_variables_initializer을 통해 시작 변수를 초기화해주어야 한다.
sess = tf.Session()
sess.run(tf.global_variables_initializer())
# W 가중치, Cost를 담을 리스트 생성
W_list = []
b_list = []
cost_list = []
step_list = []
for step in range(2001):
cost_val, W_val, b_val, _ = sess.run([cost, W, b, train],
feed_dict = {X:[1, 2, 3, 4, 5],
Y:[2.1, 3.1, 4.1, 5.1, 6.1]})
if step%20 == 0:
step_list.append(step)
W_list.append(W_val)
cost_list.append(cost_val)
b_list.append(b_val)
print(step, cost_val, W_val, b_val)
plt.plot(step_list, b_list)
plt.show()
plt.plot(step_list, W_list)
plt.show()
plt.plot(step_list, cost_list)
plt.show()