잘못된 내용은 언제든지 밑의 댓글로 알려주세요!

Multi-Variable Regression

기본적인 Linear Regression은 독립변수인 X와 종속변수인Y가 하나씩 있는 선형 회귀관계 였습니다. 그러나 실제 Regression 모델을 만들 때에는 독립변수와 종속변수가 1:1 관계에 있는 경우는 매우 드문 경우입니다. 따라서 이번 포스팅에서는 변수가 여러개일 경우에 사용하는 Multi-Variable Regression에 대해서 알아보겠습니다.

1. Hypothesis와 Cost 함수.

먼저 Linear Regression과 동일하게 Hypothesis와 Cost함수를 살펴보겠습니다.

Multi-variable regression Hypothesis	cost 함수

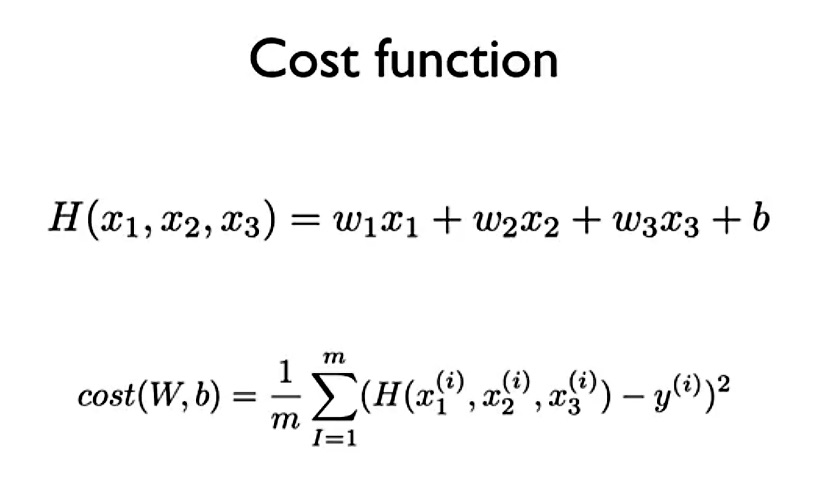위의 Hypothesis와 Cost함수를 보면 Linear Regression과 매우 비슷함을 알 수 있습니다. 차이가 있다면 Linear Regression에서는 독립변수가 X 하나였다면, Multi-variables Regression에서는 여러개라는 것입니다.

2. 행렬 연산을 위한 데이터 차원 수

종속변수와 독립변수가 1:1 관계인 Linear Regression에서는 차원 수를 크게 고려하지 않지만 Multi-variables Regression에서는 차원 수를 필수적으로 고려해주어야 합니다. 그 이유는 행렬 연산 때문인데, 다음 공식을 보겠습니다.

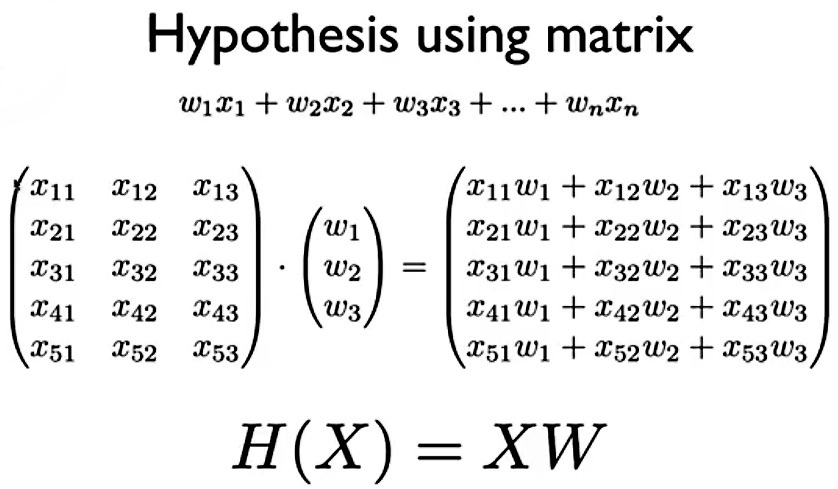
tensorflow를 이용한 딥러닝에서 Cost함수의 값을 좌지우지 하는 것은 W매트릭스입니다. 그렇기에 W를 Linear Regression에서는 다음과 같은 코드로 설정합니다.

W = tf.Variable(tf.random_normal([1]), name = 'weight')

여기서 주목해야 할 것은 [ ]속에 담겨진 숫자 입니다. Linear Regression에서는 X가 1차원 데이터이기 때문에 단순히 ‘[1]’로 설정하면 됐지만, X의 차원이 달라지면 ‘[ ]’안에 들어가는 차원도 달라져야 합니다. 위 그림의 Matrix에서는 X가 [5, 3]차원이기 때문에 W가 [3, 1]차원이 되어야 최종 Hypothesis가 [5, 1]차원이 돼어, 비로소 Cost함수를 계산할 수 있는 구조가 나옵니다. 요약하면 다음과 같습니다.

종속변수 y = [5, 1]차원
독립변수 X = [5, 3]차원
W 매트릭스 = [5, 1]차원
예측 y_hat = [5, 1차원
Cost = tf.reduce_mean(tf.square(y_hat - y))

3. Tensorflow 코드

입력 차원에 따라 W의 차원이 바뀐다는 것만 알면 나머지 연산은 Linear Regression과 크게 다르지 않습니다. 코드를 바로 보겠습니다. 캐글에서 집값을 예측하는 데이터를 가져왔습니다. 그리고 주의해야 할 것은 tensorflow연산 시 입력 데이터 안에는 절대 NAN값이 없어야 합니다.

3-1. 데이터 load

import numpy as np
import pandas as pd
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_absolute_error

tf.set_random_seed(777)  # for reproducibility

data = pd.read_csv('/train.csv')

# 독립변수
data_x = data[['MSSubClass', 'LotArea', 'OverallQual', 'OverallCond', 
'YearBuilt', 'YearRemodAdd', 'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF']]
# 종속변수(집값)
data_y = data[['SalePrice']]

3-2. 데이터 Scale 조정

Scale을 조정할 때에는 X와 Y따로 Scaler를 만드는 것을 추천합니다. 이유는 Scaler를 따로 만들어야 나중에 inverse_transform함수를 통해 원래의 스케일로 변환할 수 있기 때문입니다.

# X data 스케일 조정
scaler_x = StandardScaler()
scaler_x.fit(data_x)
data_x_scaled = scaler_x.transform(data_x)
data_x_scaled = pd.DataFrame(data_x_scaled)
data_x_scaled.columns = data_x.columns

# Y data 스케일 조정
scaler_y = StandardScaler()
scaler_y.fit(data_y)
data_y_scaled = scaler_y.transform(data_y)
data_y_scaled = pd.DataFrame(data_y_scaled)
data_y_scaled.columns = data_y.columns

3-3. Tensorflow 적용

이 과정에서 이해 안되는 부분은 Linear Regression를 참고하면 이해가 되실겁니다.

# pandas to numpy
x_data = data_x_scaled.to_numpy(dtype='float32')
y_data = data_y_scaled.to_numpy(dtype='float32')
# x_data = df[:, 0:-1]
# y_data = df[:, [-1]]

# X, Y, W, b 설정
X = tf.placeholder(tf.float32, shape = [None, 9])
Y = tf.placeholder(tf.float32, shape = [None, 1])

W = tf.Variable(tf.random_normal([9, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

# hypothesis
hypothesis = tf.matmul(X, W) + b

# Simplified cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))

# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)
train = optimizer.minimize(cost)

sess = tf.Session()
# Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())

cost_list = []
step_list = []
y_list = []
y_pred_list = []
mae_cv = []

for step in range(100001):
    cost_val, hy_val, _ = sess.run(
        [cost, hypothesis, train], feed_dict={X: x_data, Y: y_data})
    if step % 10 == 0:
        # 예측값 scale 반전
        inv_hy_val = scaler_y.inverse_transform(hy_val)
        # 실제값 scale 반전
        inv_y_data = scaler_y.inverse_transform(y_data)
        # mae 계산
        mae = mean_absolute_error(inv_y_data, inv_hy_val)
        mae_cv.append(mae)
        cost_list.append(cost_val)
        step_list.append(step)
        print('step:', step)

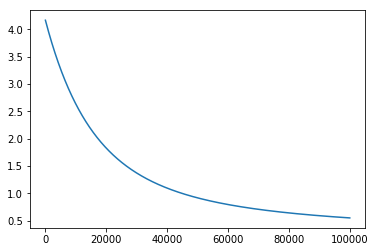
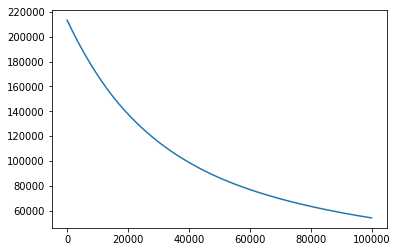
3-4. 결과

Step에 따른 Cost값	Step에 따른 MAE값

tensorflow를 통해 100,000번 연산을 진행한 결과 cost값이 점점 감소하는 것을 알 수 있습니다. 그러나 Scale을 변환했기 때문에 학습이 된다는 것은 알겠는데 학습이 어느정도로 잘 되었는지는 체감하기 어렵습니다.

# 예측값 scale 반전
nv_hy_val = scaler_y.inverse_transform(hy_val)
# 실제값 scale 반전
inv_y_data = scaler_y.inverse_transform(y_data)
# mae 계산
mae = mean_absolute_error(inv_y_data, inv_hy_val)
mae_cv.append(mae)

그래서 위의 코드에서 실제값과 예측값의 차이를 의미하는 MAE를 스케일 변환한 값을 이용하여 구해주었습니다. 그 결과 예측값은 100,000번의 학습 끝에 60,000원 정도의 차이로 집값을 예측함을 알 수 있습니다. 다음의 공식으로 MAPE를 구해보면 약 65%의 정확도가 나옴을 알 수 있습니다.

error = np.mean(np.abs((inv_y_data - inv_hy_val) / inv_y_data)) * 100
Accuracy = 100 - error

이상으로 Multi-Variable Regression 설명과 Code 구현을 마치겠습니다.

reference

모두의 딥러닝

Multi-variable Regression with Tensorflow

데이터 차원에 대한 중요성