Logistic Regression 로지스틱 회귀분석 Cross-Entropy Tensorflow 모두의 딥러닝 Gradien Descent Data Analysis

Logistic Regression with Tensorflow

sigmoid 함수에 대한 이해를 바탕으로

Posted by Minki on May 14, 2020

잘못된 내용은 언제든지 밑의 댓글로 알려주세요!

Logistic Regression

1. 선형회귀분석과 차이점

이번 포스팅에서는 독립변수인 X와 종속변수인 Y가 1:1 관계에 있는 Logistic Regression에 대해서 설명하겠습니다. 로지스틱 회귀분석은 선형 회귀 분석과 같은 1:1 관계지만 종속변수인 Y에 아주 큰 차이점이 있습니다. 차이점은 다음과 같습니다.

  • 선형회귀분석의 Y : 몸무게, 키 등 숫자로 표현됨.
  • 로지스틱회귀분석의 Y : True or False 혹은 1 or 0과 같이 binary 형태로 표현됨.

이렇게 예측하고자 하는 Y값에 큰 차이점이 있기 때문에, 당연히 로지스틱 회귀분석을 구성하는 Hypothesis나 Cost에도 차이점이 존재합니다. 차근차근 살펴보겠습니다.

2. Hypothesis와 Cost

우선 Logistic Regression의 Hypothesis와 cost는 다음과 같습니다.

2-1. Hypothesis


\[H(x) = {1 \over (1+e^{-W^TX})}\]


위의 Hypothesis에서 주목할 것은 Sigmoid함수로 불리는 \(S(z) = {1 / (1+e^{-z})}\)입니다. 비선형 및 선형 회귀분석에서는 Sigmoid 함수를사용하지 않고, Hypothesis를 단순히 \(H(x) = XW\)로 표현했습니다. 그리고 이 식의 \(XW\)는 \(W^TX\)와 같은 공식입니다. 그렇다면 왜 \(W^TX\)를 \(S(z)\)의 \(z\)에 대입한 것일까요? 이를 위해 Sigmoid 그래프를 보도록 하겠습니다.

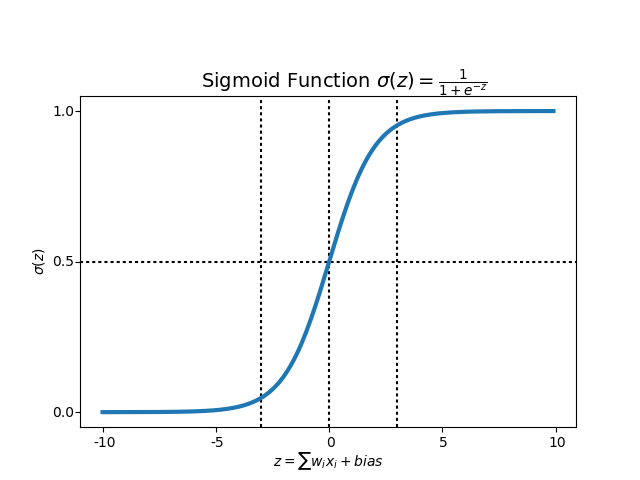
위에서 보다시피 Sigmoid함수는 \(W^TX\)의 모든 값을 0과 1사이의 값으로 만들어 줍니다. 그래서 만약 Hypothesis의 임계치인 Threshold를 위의 \(\alpha(Z)\)의 값인 0.5로 설정한다면 다음과 같이 binary 값인 \(Y\)를 예측할 수 있게됩니다.

  1. \(H(x) = {1 \over (1+e^{-W^TX})}\) >= 0.5라면, \(Y\) 값을 1로 예측
  2. \(H(x) = {1 \over (1+e^{-W^TX})}\) < 0.5라면, \(Y\) 값을 0으로 예측

따라서 이와같이 \(Y\)함수를 예측하기 위해 Sigmoid함수를 사용해서 Hypothesis를 구하는 것입니다.

2-2. Cross-Entropy(=Cost)


\[Cost(W) =\] \[{-1 \over m}\sum y log(H(x)) + (1-y)(log(1-H(x)))\]


이제 \(Y\)의 예측값을 구했으므로 \(Cost\)값을 tensorflow 연산으로 지속적으로 감소시켜야 합니다. 이를 위해서 예측값이 정답일 경우 \(Cost\)값을 매우 작게, 예측값이 오답일 경우 \(Cost\)값을 매우 크게 만드는 것이 중요합니다. 그리고 이는 위에 나와있는 \(Cost(W)\)식으로 구현할 수 있습니다. \(y\)값에 따른 \(Cost(W)\)식을 보겠습니다.

1. \(y=1\)일 경우


\[Cost(H(x), y) = -log(H(x))\]


  1. \(H(x) = 1\), 즉 정답일 경우는 \(Cost(H(x), y) = 0\) => 매우 작다
  2. \(H(x) = 0\), 즉 오답일 경우는 \(Cost(H(x), y) = \infty\) => 매우 크다

2. \(y=0\)일 경우


\[Cost(H(x), y) = (log(1-H(x)))\]


  1. \(H(x) = 1\), 즉 오답일 경우는 \(Cost(H(x), y) = \infty\) => 매우 크다
  2. \(H(x) = 0\), 즉 정답일 경우는 \(Cost(H(x), y) = 0\) => 매우 작다

따라서 이를 통해 \(Cost(W)\)함수 역시 잘 작동함을 알 수 있습니다.

2-3. Gradient Descent


\[W := {W - \alpha {\sigma \over \sigma W}cost(W)}\]


Gradient Descent 함수는 선형 회귀분석과 같게, Gradient가 기울기의 방향대로 감소함을 알 수 있습니다. 이제 위의 과정을 코드로 구성해보겠습니다.

3. Tensorflow code 구현

3-1. 데이터 로드 및 Placeholder & Variable 설정

가장 먼저 데이터를 불러온 뒤에 가장 기본이 되는 X, Y, W, b를 tensor로 지정해줍니다. X, Y, W, b를 설정할 시에 데이터의 차원에 항상 주의해줍니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import matplotlib.pyplot as plt
import numpy as np

tf.set_random_seed(777)  # for reproducibility

# 데이터 로드
xy = np.loadtxt('/diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]

# placeholders for a tensor that will be always fed.

X = tf.placeholder(tf.float32, shape=[None, 8])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([8, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

3-2. Hypothesis와 Cost 함수

그 다음 logistic regression이므로 시그모이드 함수를 활용하여 Hypothesis와 Cost함수를 지정해줍니다.

1
2
3
4
5
6

# hypothesis function
# 선형회귀분석과는 다르게 tf.sigmoid가 추가되었습니다.
hypothesis = tf.sigmoid(tf.matmul(X, W) + b)
# cost/loss function
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) * tf.log(1 - hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)

3-2. Predicted와 Accuracy 함수

Predicted에서 tf.cast 함수를 사용해 임계치(Threshold)보다 큰 값을 True, 1, 작은 값을 False, 0으로 변환해줍니다.

1
2
3
4

# Accuracy computation
# True if hypothesis>0.5 else False, True = 1, False = 0
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))

3-3. 최종 학습 진행

최종 학습 과정은 일반적인 선형회귀분석과 비슷합니다. 다만 다른점이 있다면, Predicted와 Accracy를 산출하는 방법입니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

cost_list = []
step_list = []
acc_list = []

# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())

    for step in range(10001):
        cost_val, _, h, c, a = sess.run([cost, train, hypothesis, predicted, accuracy], 
                                        feed_dict={X: x_data, Y: y_data})
        if step % 100 == 0:
            step_list.append(step)
            cost_list.append(cost_val)
            acc_list.append(a)
    
    # 최종 cost 출력
    print("\nCost: ", cost_val, "\nAccuracy: ", a)

4. 최종 결과

최종 결과를 그래프로 살펴보면 다음과 같습니다.

1
2

plt.plot(step_list, cost_list)
plt.plot(step_list, acc_list)
Cost graph Accuracy Graph

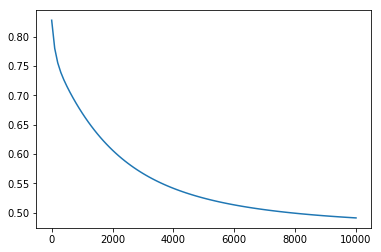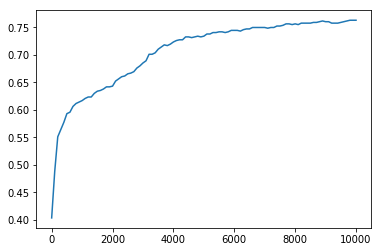위 그래프에서도 알 수 있듯이, 학습이 진행될 수록 \(cost\)값은 줄어들고, \(Accuracy\)값은 증가하는 것을 볼 수 있습니다. 이로써 모델이 학습을 성공적으로 수행함을 확인할 수 있습니다.

4-1. 학습된 모델을 테스트 하려면?

학습된 모델을 테스트 하려면 with tf.Session() as sess:구문을 사용하면 안됩니다. 그 이유는 with구문은 구문이 끝나면 sess를 저장하지 않고 삭제하기 때문입니다. 따라서 학습된 모델을 바꾸고 테스트하고 싶다면 마지막 코드를 다음과 같이 바꾸어야 합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

cost_list = []
step_list = []
acc_list = []

# Launch graph
sess = tf.Session()
# Initialize TensorFlow variables
sess.run(tf.global_variables_initializer())

for step in range(10001):
    cost_val, _, h, c, a = sess.run([cost, train, hypothesis, predicted, accuracy], 
                                    feed_dict={X: x_data, Y: y_data})
    if step % 100 == 0:
        step_list.append(step)
        cost_list.append(cost_val)
        acc_list.append(a)
            
# sess.close()
    
# 최종 cost 출력
print("\nCost: ", cost_val, "\nAccuracy: ", a)

# 테스트 값 출력

result = sess.run([hypothesis, predicted], feed_dict = {X: [[-0.294, 0.487, 0.180, -0.292, 0., 0.001, -0.531, -0.033]]})
print('Hypothsis :', result[0], 'Predicted :', result[1])


reference

CATALOG
    FEATURED TAGS
    Data Analysis Flutter 모두의 딥러닝 Tensorflow 서비스 기획 추천시스템 포스트코로나 2020 빅콘테스트 Gradien Descent MCLP Recommendation System bigcontest covid19 빅콘테스트 지수 개발 ALS Alternating Least Squares Matrix Factorization dart