잘못된 내용은 언제든지 밑의 댓글로 알려주세요!
들어가기
이번 포스팅은 딥러닝의 초입입니다. 역전파와 레이어 쌓기를 통해 XOR 문제와 MNIST Classification을 시도해보겠습니다.
1. 레이어는 왜 쌓아야 할까?
딥러닝에 관심이 많거나 공부를 조금이라도 해보신 분들은 ‘Layer’란 단어를 많이 들어보셨을 것입니다. 이처럼 ‘Layer’는 딥러닝과 뗄레야 뗄 수 없는 관계인데, 그 이유를 간단히 말씀드리면 딥러닝을 만들 때 ‘Layer’를 층층이 쌓아서 만들기 때문입니다.
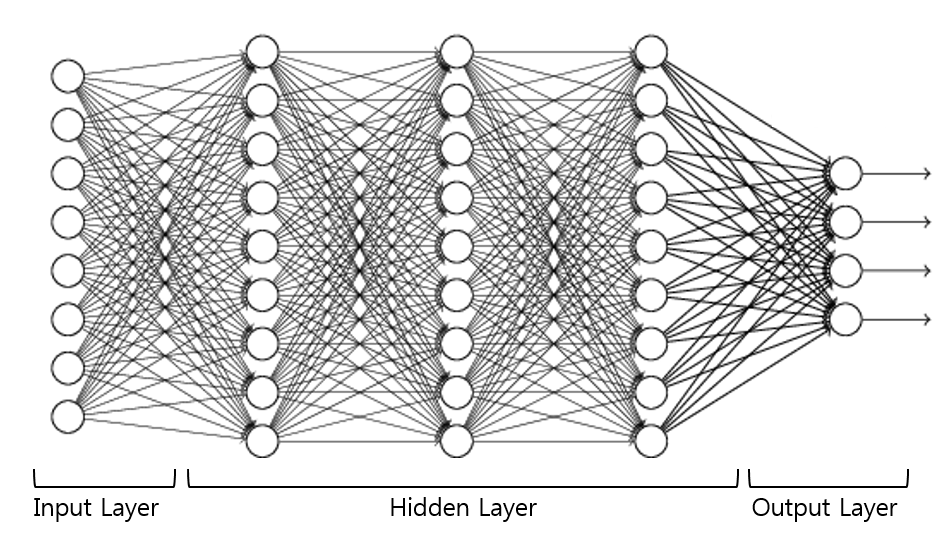
그러나 이전 포스팅에서 보았듯이 ‘로지스틱 회귀분석’과 ‘선형 회귀분석’ 등은 레이어를 쌓지 않아도 충분히 모델이 잘 학습했습니다. 그렇다면 어떤 이유 때문에 모델을 만들 때 이전과는 다르게 ‘Layer’를 층층이 쌓아야 하는 것일까요? 이를 알아보기 위해 아주 고전적인 문제인 ‘XOR’ 분류 문제를 살펴보겠습니다.
2. XOR 분류하기
‘OR’과 ‘AND’도 아니고 ‘XOR’이 무엇일까? 이는 아래 그림과 설명을 보시면 이해가 빠르실 것입니다.
- AND : 모든 원소가 1이여야 Output이 1(교집합)
- OR : 원소 중 하나라도 1이면 Output이 1(합집합)
- XOR : 원소가 다르면 Output이 1(차집합)
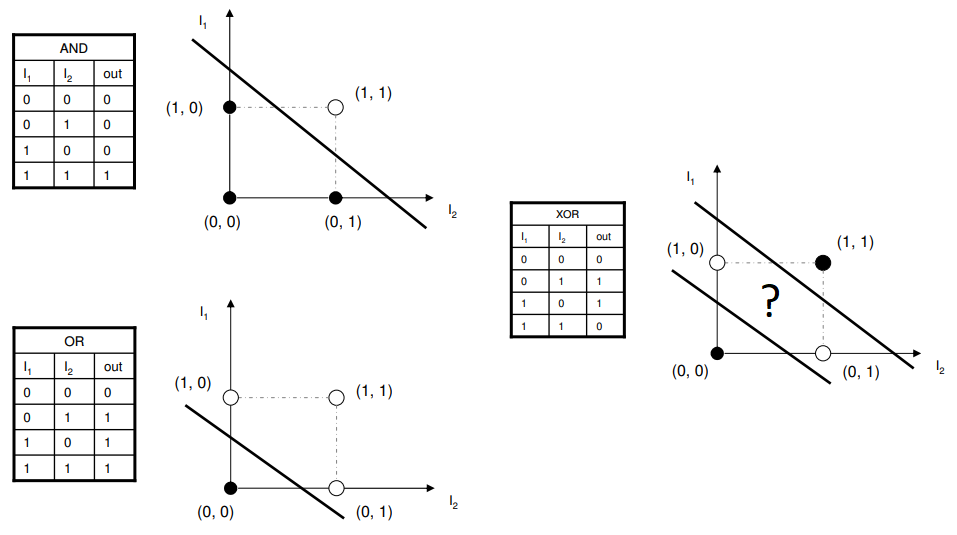
그렇다면 하나의 ‘선’을 가지고 XOR문제를 완벽하게 분류할 수 있을까요? 위 그림을 보시면 아시겠지만 불가능합니다. 실제로 불가능한지 텐서플로우로 분류를 시도해보겠습니다.
먼저 선형 분류를 진행하기 위해 다음의 코드로 Hypothesis를 생성합니다.
1
hypothesis = tf.sigmoid(tf.matmul(X, W) + b)
그 후 입력 차원에 맞춰서 X, Y, W, b Tensor를 생성할 것입니다.
1
2
3
4
X = tf.placeholder(tf.float32, [None, 2])
Y = tf.placeholder(tf.int32, [None, 1])
W = tf.Variable(tf.random_normal([2, 1]))
b = tf.Variable(tf.random_normal([1]))
2-1. 한개의 직선을 이용한 XOR 분류 결과
위의 코드로 tensor를 생성한 다음에 분류를 진행하면 우리의 모델은 직선 한개로 XOR문제를 분류하려고 시도할 것입니다. 그러나 아래의 그래프에서 볼 수 있듯이 아무리 많이 학습을 시켜도 단일 시그모이드로는 XOR 분류 문제를 해결할 수 없습니다.
| Cost 그래프 | Accuracy 그래프 |
|---|---|
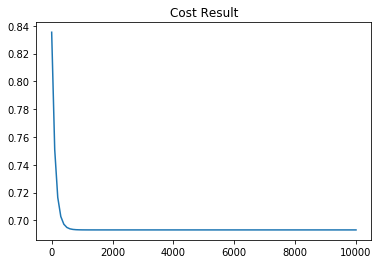 |
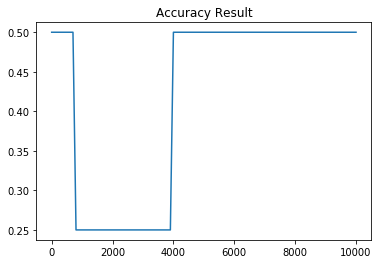 |
그럼 어떻게 XOR분류 문제를 해결할 수 있을까요? 정말 간단하게 생각하면 정답은 쉽습니다. 정답은 바로 ‘하나의 직선을 사용하는 것이 아닌 두개 이상의 직선을 사용한다.’입니다. 그리고 두개 이상의 직선을 생성해내는 방법이 ‘Layer’를 층층이 쌓는 방법입니다. 이제 왜 딥러닝에서 ‘Layer’가 중요한지 느껴지시나요? 그럼 지금부터 Layer 쌓는 방법에 대해 알아보겠습니다.
3. Gradient와 레이어
일반적으로 신경망 퍼셉트론은 학습을 위해 Gradient Descent를 사용합니다. Gradient Descent에서 Gradient가 하는 역할은 모델에게 Cost를 감소시킬 수 있는 방향을 알려줌으로써,
모델이 다음단계에 global minimum에 조금 더 다가갈 수 있게 해주는 것입니다.
이처럼 모델은 학습을 위해 Gradient를 필요로 합니다. 이런 과점에서 제가 위에서 말한 두개의 직선의 의미를 말씀드리자면, 바로 하나의 퍼셉트론이 얻어낸 Gradient를 ‘Layer’란 통로를 통해 다른 퍼셉트론으로 전달한다는 말입니다.
3-1. Sigmoid Layer로 Neural NetWork 구현
그럼 이제 한 시그모이드에서 얻은 Gradient를 다른 시그모이드로 전달하기 위한 텐서플로우 코드를 짜보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
x_data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]], dtype=np.float32)
y_data = np.array([[0], [1], [1], [0]], dtype=np.float32)
X = tf.placeholder(tf.float32, [None, 2])
Y = tf.placeholder(tf.float32, [None, 1])
W1 = tf.Variable(tf.random_normal([2, 2]), name='weight1')
b1 = tf.Variable(tf.random_normal([2]), name='bias1')
layer1 = tf.sigmoid(tf.matmul(X, W1) + b1)
W2 = tf.Variable(tf.random_normal([2, 1]), name='weight2')
b2 = tf.Variable(tf.random_normal([1]), name='bias2')
hypothesis = tf.sigmoid(tf.matmul(layer1, W2) + b2)
위의 코드를 보시면 W1, b1을 통해 로지스틱 Regression과 동일하게 시그모이드를 이용한 Hypothesis를 구합니다. 그리고 구해진 Hypothesis를 다음 시그모이드의 행렬 연산에 대입하면 됩니다.
이를 통해 W1의 가중치가 최종 연산까지 전달될 수 있습니다.
3-2. Sigmoid Neural NetWork 학습 결과
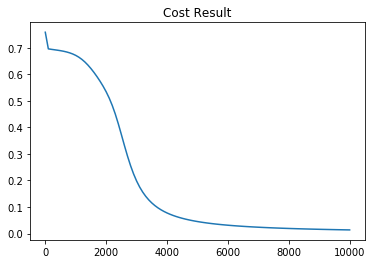
| Cost 그래프 | Accuracy 그래프 |
|---|---|
 |
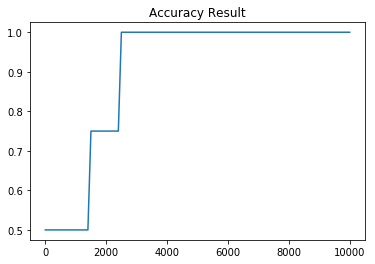 |
두개의 시그모이드로 Neural NetWork를 만들어 XOR 분류 문제를 학습시켜본 결과 하나의 시그모이드 함수를 사용했던 것과는 다르게 Neural NetWork가 안정적으로 학습을 진행한다는 것을 알 수 있습니다.
이번엔 시그모이드 레이어를 더 많이 그리고 더 깊게 연결한 Neural NetWork로 XOR 분류 문제를 시도해보겠습니다. 사용한 텐서플로우 코드는 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
W1 = tf.Variable(tf.random_normal([2, 10]), name='weight1')
b1 = tf.Variable(tf.random_normal([10]), name='bias1')
layer1 = tf.sigmoid(tf.matmul(X, W1) + b1)
W2 = tf.Variable(tf.random_normal([10, 10]), name='weight2')
b2 = tf.Variable(tf.random_normal([10]), name='bias2')
layer2 = tf.sigmoid(tf.matmul(layer1, W2) + b2)
W3 = tf.Variable(tf.random_normal([10, 10]), name='weight3')
b3 = tf.Variable(tf.random_normal([10]), name='bias3')
layer3 = tf.sigmoid(tf.matmul(layer2, W3) + b3)
W4 = tf.Variable(tf.random_normal([10, 1]), name='weight4')
b4 = tf.Variable(tf.random_normal([1]), name='bias4')
hypothesis = tf.sigmoid(tf.matmul(layer3, W4) + b4)
3-2-1. 더 큰 Sigmoid Neural NetWork 학습 결과
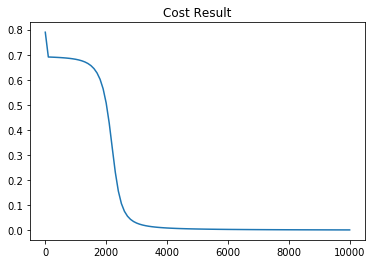
| Cost 그래프 | Accuracy 그래프 |
|---|---|
 |
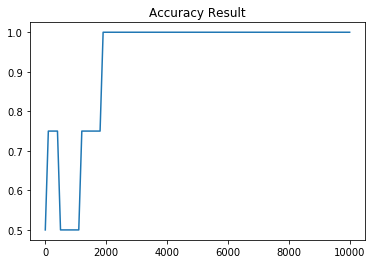 |
시그모이드 가중치를 2차원에서 10차원으로, 레이어를 두개에서 네개로 늘린 결과 아주 약간이나마 학습이 이전보다 더 빨리 진행된 것을 눈으로 보실 수 있습니다. 이처럼 레이어와 가중치 차원을 잘 조절함으로써 모델의 성능을 올릴 수 있습니다.
4. 전체 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import matplotlib.pyplot as plt
import random
import tensorflow_datasets as tfds
import numpy as np
import pandas as pd
W1 = tf.Variable(tf.random_normal([2, 10]), name='weight1')
b1 = tf.Variable(tf.random_normal([10]), name='bias1')
layer1 = tf.sigmoid(tf.matmul(X, W1) + b1)
W2 = tf.Variable(tf.random_normal([10, 10]), name='weight2')
b2 = tf.Variable(tf.random_normal([10]), name='bias2')
layer2 = tf.sigmoid(tf.matmul(layer1, W2) + b2)
W3 = tf.Variable(tf.random_normal([10, 10]), name='weight3')
b3 = tf.Variable(tf.random_normal([10]), name='bias3')
layer3 = tf.sigmoid(tf.matmul(layer2, W3) + b3)
W4 = tf.Variable(tf.random_normal([10, 1]), name='weight4')
b4 = tf.Variable(tf.random_normal([1]), name='bias4')
hypothesis = tf.sigmoid(tf.matmul(layer3, W4) + b4)
# cost/loss function
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) * tf.log(1 - hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# Accuracy computation
# True if hypothesis>0.5 else False
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))
step_list = []
cost_list = []
acc_list = []
# Launch graph
with tf.Session() as sess:
# Initialize TensorFlow variables
sess.run(tf.global_variables_initializer())
for step in range(10001):
_, cost_val, acc = sess.run([train, cost, accuracy], feed_dict={X: x_data, Y: y_data})
if step % 100 == 0:
step_list.append(step)
cost_list.append(cost_val)
acc_list.append(acc)
print(step, cost_val)
# Accuracy report
h, c, a = sess.run(
[hypothesis, predicted, accuracy], feed_dict={X: x_data, Y: y_data}
)
print("\nHypothesis: ", h, "\nCorrect: ", c, "\nAccuracy: ", a)