잘못된 내용은 언제든지 밑의 댓글로 알려주세요!

들어가기

이번 포스팅에서는 시그모이드 이외에 다양한 활성화 함수를 Neural NetWork 구현에 사용할 예정입니다. 이 포스팅을 보시기 전에 ‘Sigmoid로 Neural NetWork 구현하기’를 읽고 오시면 더 쉽게 이번 포스팅을 이해하실 수 있습니다.

1. Sigmoid가 가진 심각한 단점

XOR 분류 문제를 해결하는데 있어서 하나의 Sigmoid보다 두개의 Sigmoid를 사용하는게 더 효율적이었고, 두개보다는 세개가 더 효율적이었습니다. 그렇다면 Sigmoid로 만든 Layer를 9~10개 이상 사용해서 모델을 학습시키면 어떤 결과가 나올까요?

1-1. Sigmoid로 10 Layer Neural NetWork 만들기

Sigmoid를 10개 사용하여 Neural NetWork를 만든 후, 이를 이용하여 XOR 분류를 시도하면 다음과 같은 결과 그래프를 얻을 수 있습니다.

Cost 그래프	Accuracy 그래프

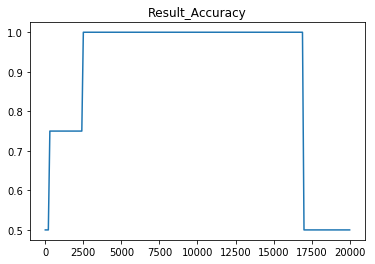위 그래프를 보면 처음에는 학습이 잘 진행되는 것처럼 보이다가, Cost가 17,500번의 학습 이후로 NaN으로 사라지게 됩니다. 그리고 Cost가 NaN으로 출력된 이후에 정확도 또한 0.5로 낮아졌습니다. 그렇다면 이런 현상이 왜 발생한 것일까요?

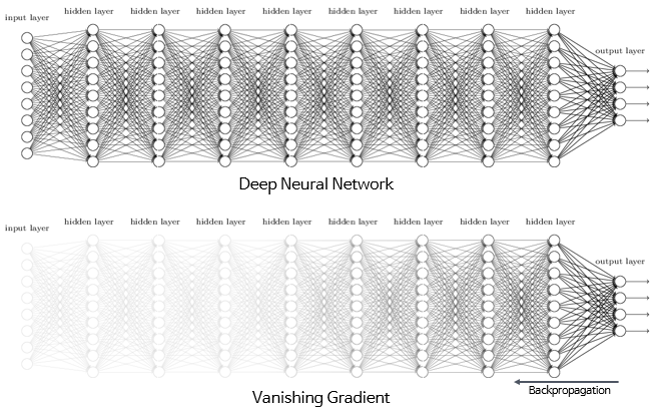
2. Vanishing Gradient

방금 전의 상황처럼 학습이 진행되다가 Cost값이 NaN이 된 이유는 쉽게 말해 Cost가 나아가야 할 방향을 알려주는 Gradient가 사라졌기 때문입니다. 그리고 이 문제를 딥러닝에서 Vanishing Gradient라고 부릅니다.

2-1. Back Propagation

그렇다면 Vanishing Gradient가 발생하는 원인은 무엇일까요? 이를 알기 위해서는 Back Propagation, 즉 역전파 현상을 이해하셔야 합니다.

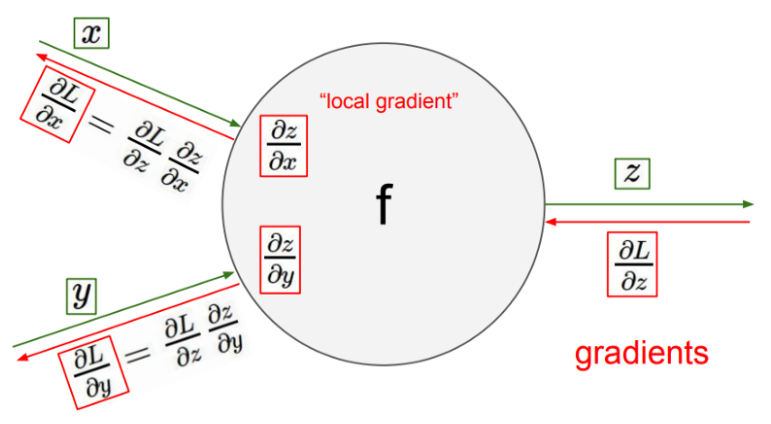
위 그림에서 초록선은 순전파(Forward Propagation), 빨간선은 역전파(Back Propagation)를 의미합니다. 또한 그림의 요소들이 의미하는 바는 다음과 같습니다.

\(L\) : 최종 출력
\(\displaystyle \frac{\partial L}{\partial x}\) : \(x\)가 \(L\)에 미치는 영향
\(\displaystyle \frac{\partial L}{\partial y}\) : \(y\)가 \(L\)에 미치는 영향
\(\displaystyle \frac{\partial L}{\partial z}\) : \(z\)가 \(L\)에 미치는 영향
\(\displaystyle \frac{\partial z}{\partial x}\) : \(z\)가 \(L\)에 미치는 영향(순전파에서 구해지는 값)
\(\displaystyle \frac{\partial z}{\partial y}\) : \(z\)가 \(L\)에 미치는 영향(순전파에서 구해지는 값)
\(Z = {f(x, y)}\) : \(x, y\)의 \(f\)연산에 의해 \(Z\)생성

위 요소들 중에서 딥러닝이 최종적으로 알아내야 하는 값은 \(\displaystyle \frac{\partial L}{\partial x}\)과 \(\displaystyle \frac{\partial L}{\partial y}\)입니다. 이를 위해서 미분을 통한 Chain Rule을 사용하는데 이 과정은 다음과 같습니다.

순전파 진행을 통해 최종 출력값인 \(L\) 계산
\(L = {g(z)}\)임을 가정하고, \(\displaystyle \frac{\partial L}{\partial z}\)를 계산(\(g\)는 \(f\)처럼 함수 형태)
\(\displaystyle \frac{\partial L}{\partial x} = \displaystyle \frac{\partial L}{\partial z} * \displaystyle \frac{\partial z}{\partial x}\)를 통해 \(\displaystyle \frac{\partial L}{\partial x}\)를 계산 (y역시 같은 과정)

따라서 위의 순전파/역전파를 통해 \(\displaystyle \frac{\partial L}{\partial x}\)와 \(\displaystyle \frac{\partial L}{\partial y}\)를 얻어 최종적으로 가중치를 학습하는 것입니다.

2-2. Sigmoid를 이용한 Back Propagation 문제점

자 그렇다면 Neural NetWork에서 Layer가 많아진다면 어떻게 될까요? 바로 \(\displaystyle \frac{\partial L}{\partial x}\)와 \(\displaystyle \frac{\partial L}{\partial y}\)를 구하기 위한 역전파 과정이 많아집니다. 따라서 역전파 과정 중에 곱해지는 가중치 또한 많아진다고 할 수 있습니다.

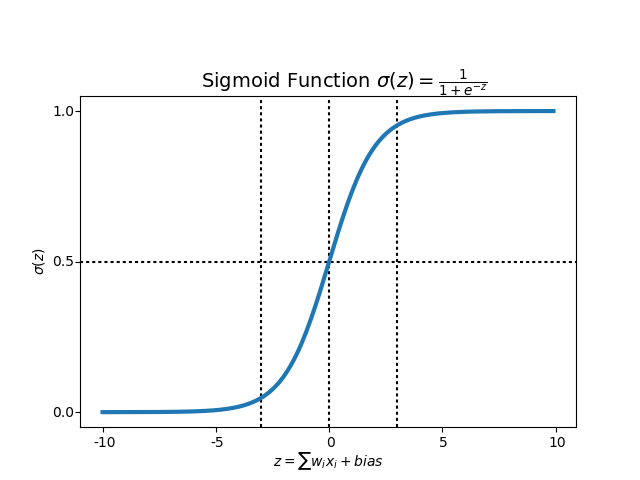
그러나 위의 그래프에서 알 수 있듯이 Sigmoid함수는 항상 0 ~ 1의 값을 가집니다. 그럼 이제 3개의 sigmoid 레이어와 10개의 sigmoid 레이어를 가진 Neural NetWork 함수의 가중치를 살펴보면 다음과 같습니다. 이해를 위해 역전파 가중치(ex. \(\displaystyle \frac{\partial z}{\partial x}\), \(\displaystyle \frac{\partial z}{\partial y}\)) 를 0.1로 가정하겠습니다.

Sigmoid 3개 layer = \(0.1*0.1*0.1 = 0.001\)
Sigmoid 10개 layer = \(0.1*0.1*0.1 \cdots *0.1 = 0.00000000001\)

Sigmoid 10개 layer로 얻어진 역전파 가중치는 거의 0에 수렴합니다. 이로 인해 \(x\)와 \(y\)가 \(L\)에 미치는 영향이 0에 가깝다는 결과가 나올 것입니다. 따라서 아무리 긴 레이어를 사용해서 학습한다 할지라도 중간에 가중치가 0으로 사라져서 학습이 안되는 현상이 발생합니다. 그렇다면 이런 Vanishing Gradient현상을 어떻게 해결할 수 있을까요?

3. Sigmoid 이외에 다양한 활성화함수

Vanishing Gradient 문제를 해결하기 위한 방법은 간단합니다. 바로 Gradient를 사라지지 않도록 하는 것입니다. 이를 위해 Sigmoid와는 다른 활성화함수를 사용해야만 합니다. 우선 Sigmoid 이외의 다양한 활성화함수를 살펴보면 다음과 같습니다.

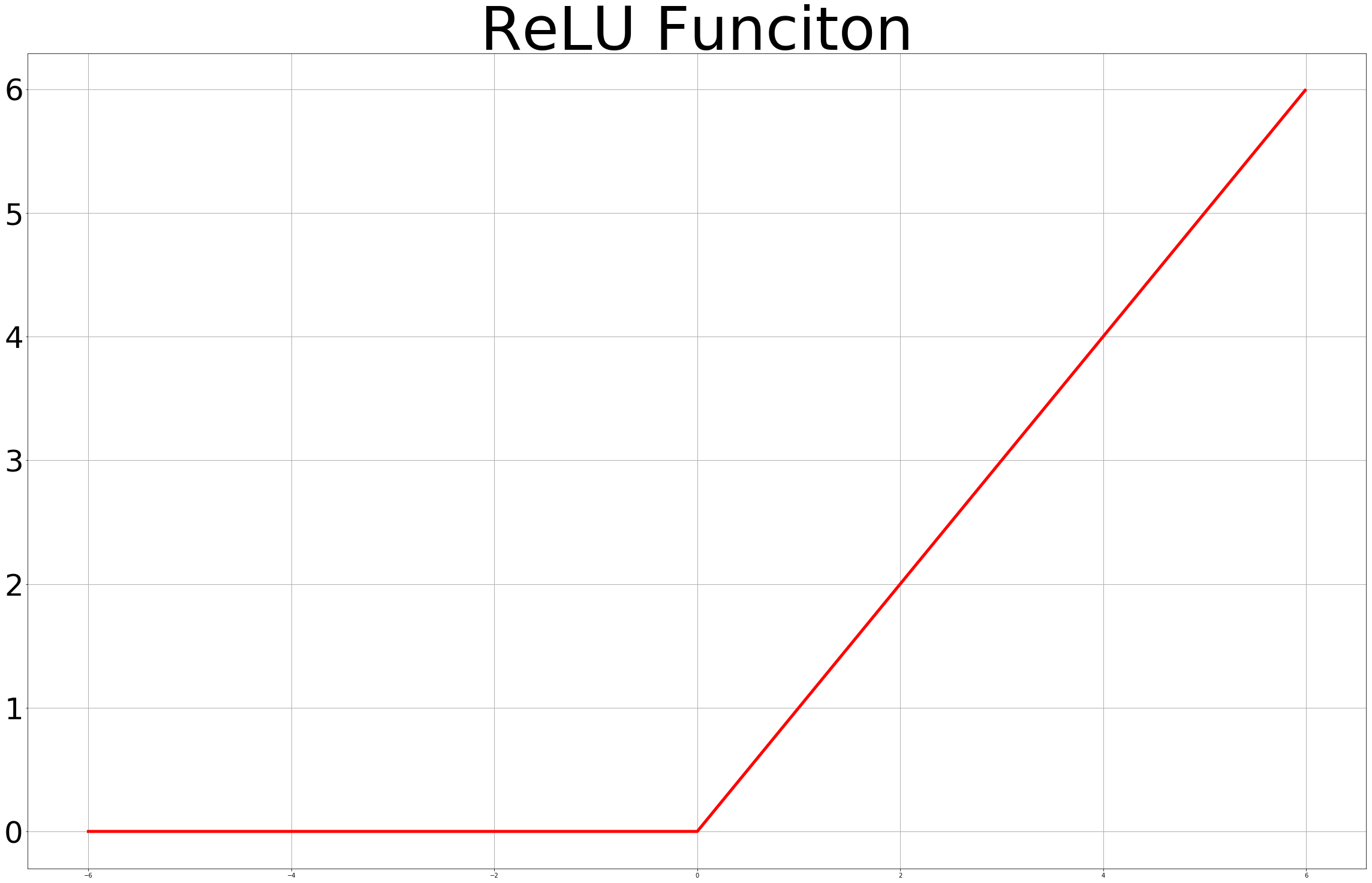
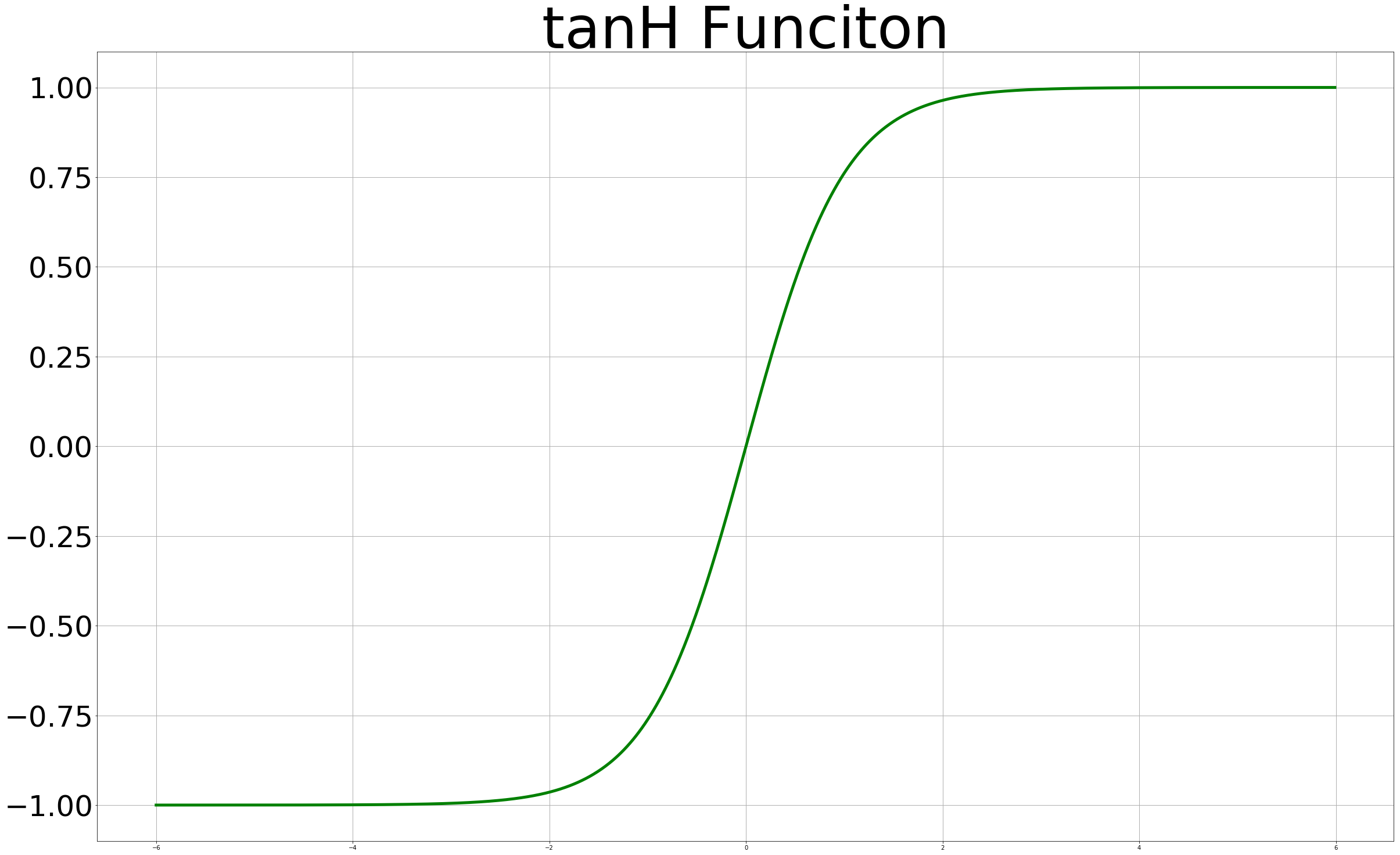
Relu 그래프	Tanh 그래프	Leacky Relu 그래프

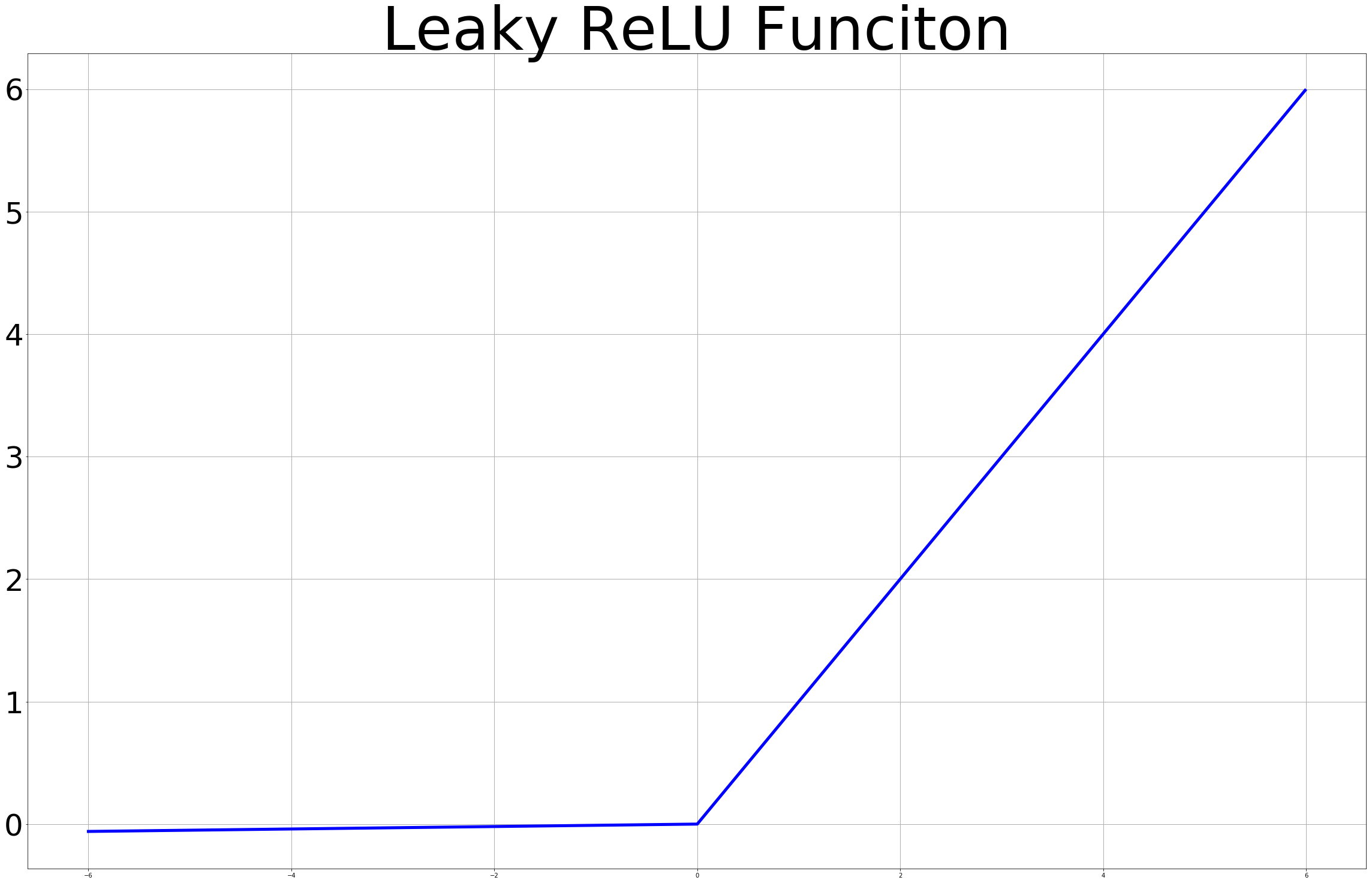0 ~ 1사이의 범위로 한정되었던 Sigmoid 함수와는 다르게 Y축으로 넓은 범위를 갖는 활성화함수를 사용함으로써 Vanishing Gradient를 해결할 수 있습니다. 이제 이 활성화 함수를 사용하여 10 Layer Nueral NetWork를 만들어 XOR 분류에 적용해보겠습니다.

3-1. 활성화함수 학습 결과

먼저 활성화 함수에 사용된 코드는 다음과 같습니다. 여기서 주의해야할 것은 마지막 출력은 0 ~ 1이 되어야하기 때문에 Sigmoid로 Hypothesis를 코딩해주어야 합니다.

# ReLU
hid8 = tf.nn.relu(tf.matmul(hid7, W8) + b8)
hid9 = tf.nn.relu(tf.matmul(hid8, W9) + b9)

# Leacky_ReLU
hid8 = tf.nn.leaky_relu(tf.matmul(hid7, W8) + b8)
hid9 = tf.nn.leaky_relu(tf.matmul(hid8, W9) + b9)

# tanh
hid8 = tf.math.tanh(tf.matmul(hid7, W8) + b8)
hid9 = tf.math.tanh(tf.matmul(hid8, W9) + b9)

# hypothesis는 Sigmoid
hypothesis = tf.sigmoid(tf.matmul(hid9, W10) + b10)

Relu 정확도	Tanh 정확도	Leacky Relu 정확도

이처럼 위의 결과를 보시면 아시겠지만 Sigmoid 함수를 사용해서 학습을 진행했던 것과는 다르게 모든 활성화 함수가 성공적으로 학습과 분류를 진행했습니다. 실제로 딥러닝 구현에서는 ReLU함수와 Leacky ReLU함수를 많이 사용하니 이 점을 꼭 기억해주시면 좋을것 같습니다.

4. 전체코드

import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import matplotlib.pyplot as plt
import random
import tensorflow_datasets as tfds
import numpy as np
import pandas as pd

x_data = np.array([[0,0], [0,1], [1,0], [1,1]], dtype=np.float32)
y_data = np.array([[0],[1],[1],[0]], dtype=np.float32)

X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W1 = tf.Variable(tf.random_normal([2,5]), name='weight1')
W2 = tf.Variable(tf.random_normal([5,5]), name='weight2')
W3 = tf.Variable(tf.random_normal([5,5]), name='weight3')
W4 = tf.Variable(tf.random_normal([5,5]), name='weight4')
W5 = tf.Variable(tf.random_normal([5,5]), name='weight5')
W6 = tf.Variable(tf.random_normal([5,5]), name='weight6')
W7 = tf.Variable(tf.random_normal([5,5]), name='weight7')
W8 = tf.Variable(tf.random_normal([5,5]), name='weight8')
W9 = tf.Variable(tf.random_normal([5,5]), name='weight9')
W10 = tf.Variable(tf.random_normal([5,1]), name='weight10')

b1 = tf.Variable(tf.random_normal([5]), name='bias1')
b2 = tf.Variable(tf.random_normal([5]), name='bias2')
b3 = tf.Variable(tf.random_normal([5]), name='bias3')
b4 = tf.Variable(tf.random_normal([5]), name='bias4')
b5 = tf.Variable(tf.random_normal([5]), name='bias5')
b6 = tf.Variable(tf.random_normal([5]), name='bias6')
b7 = tf.Variable(tf.random_normal([5]), name='bias7')
b8 = tf.Variable(tf.random_normal([5]), name='bias8')
b9 = tf.Variable(tf.random_normal([5]), name='bias9')
b10 = tf.Variable(tf.random_normal([1]), name='bias10')

# # Sigmoid
# hid1 = tf.sigmoid(tf.matmul(X, W1) + b1)
# hid2 = tf.sigmoid(tf.matmul(hid1, W2) + b2)
# hid3 = tf.sigmoid(tf.matmul(hid2, W3) + b3)
# hid4 = tf.sigmoid(tf.matmul(hid3, W4) + b4)
# hid5 = tf.sigmoid(tf.matmul(hid4, W5) + b5)
# hid6 = tf.sigmoid(tf.matmul(hid5, W6) + b6)
# hid7 = tf.sigmoid(tf.matmul(hid6, W7) + b7)
# hid8 = tf.sigmoid(tf.matmul(hid7, W8) + b8)
# hid9 = tf.sigmoid(tf.matmul(hid8, W9) + b9)

# # relu!!
# hid1 = tf.nn.relu(tf.matmul(X, W1) + b1)
# hid2 = tf.nn.relu(tf.matmul(hid1, W2) + b2)
# hid3 = tf.nn.relu(tf.matmul(hid2, W3) + b3)
# hid4 = tf.nn.relu(tf.matmul(hid3, W4) + b4)
# hid5 = tf.nn.relu(tf.matmul(hid4, W5) + b5)
# hid6 = tf.nn.relu(tf.matmul(hid5, W6) + b6)
# hid7 = tf.nn.relu(tf.matmul(hid6, W7) + b7)
# hid8 = tf.nn.relu(tf.matmul(hid7, W8) + b8)
# hid9 = tf.nn.relu(tf.matmul(hid8, W9) + b9)

# # leacky relu!!
# hid1 = tf.nn.leaky_relu(tf.matmul(X, W1) + b1)
# hid2 = tf.nn.leaky_relu(tf.matmul(hid1, W2) + b2)
# hid3 = tf.nn.leaky_relu(tf.matmul(hid2, W3) + b3)
# hid4 = tf.nn.leaky_relu(tf.matmul(hid3, W4) + b4)
# hid5 = tf.nn.leaky_relu(tf.matmul(hid4, W5) + b5)
# hid6 = tf.nn.leaky_relu(tf.matmul(hid5, W6) + b6)
# hid7 = tf.nn.leaky_relu(tf.matmul(hid6, W7) + b7)
# hid8 = tf.nn.leaky_relu(tf.matmul(hid7, W8) + b8)
# hid9 = tf.nn.leaky_relu(tf.matmul(hid8, W9) + b9)

# leacky relu!!
hid1 = tf.math.tanh(tf.matmul(X, W1) + b1)
hid2 = tf.math.tanh(tf.matmul(hid1, W2) + b2)
hid3 = tf.math.tanh(tf.matmul(hid2, W3) + b3)
hid4 = tf.math.tanh(tf.matmul(hid3, W4) + b4)
hid5 = tf.math.tanh(tf.matmul(hid4, W5) + b5)
hid6 = tf.math.tanh(tf.matmul(hid5, W6) + b6)
hid7 = tf.math.tanh(tf.matmul(hid6, W7) + b7)
hid8 = tf.math.tanh(tf.matmul(hid7, W8) + b8)
hid9 = tf.math.tanh(tf.matmul(hid8, W9) + b9)

# 마지막은 sigmoid
hypothesis = tf.sigmoid(tf.matmul(hid9, W10) + b10)

cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) * tf.log(1 - hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)

predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))

cost_list = []
step_list = []
acc_list = []

# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())

    for step in range(20001):
        _, cost_val, acc = sess.run([train, cost, accuracy], feed_dict={X: x_data, Y: y_data})
        if step % 100 == 0:
            step_list.append(step)
            cost_list.append(cost_val)
            acc_list.append(acc)
            print(step, cost_val)
            

    # Accuracy report
    h, p, a = sess.run(
        [hypothesis, predicted, accuracy], feed_dict={X: x_data, Y: y_data}
    )
    
    print(f"\nHypothesis:\n{h} \nPredicted:\n{p} \nAccuracy:\n{a}")

reference

모두의 딥러닝

Vanishing Gradient와 ReLU 함수

다양한 활성화함수에 대한 비교