잘못된 내용은 언제든지 밑의 댓글로 알려주세요!

들어가기

이번 포스팅에서는 기본적인 implicit 데이터를 생성해보고 이를 Collaborative Filtering의 일종인 Matrix Factorization을 이용한 추천시스템을 구현해보겠습니다. 이번 포스팅은 이 글을 참조하였습니다.

1. Latent Matrix

Matrix Factorization을 구현할 때, latent matrix라는 단어가 많이 언급됩니다. 그렇다면 latent matrix란 무엇일까요?

latent란 우리말로 ‘잠재된’을 의미합니다. 이전 포스팅에서 Collaboratice Filtering을 설명하면서 실제 서비스에서는 사용자가 평가한 항목보다 그렇지 않은 항목이 훨씬 더 많다고 언급한바 있습니다.

결국 이 말은 행렬에 잠재(latent) 요인이 매우 많다는 것입니다. 따라서 Latent Matrix는 이런 잠재 요인을 기반으로 만들어진 행렬을 의미합니다. 그렇다면 이제 Matrix Factorization을 살펴보도록 하겠습니다.

2. Matrix Factorization

Row에는 유저, Column에는 아이템, 그리고 element로는 평점을 가지는 Matrix가 있습니다. 그렇다면 잠재 요인은 유저를 기반으로 하나가 생기고, 또 아이템을 기반으로 하나가 생기게 됩니다. 그럼 이제 두 잠재요인을 기반으로 하나의 행렬을 아래의 그림처럼 분해해 보겠습니다.

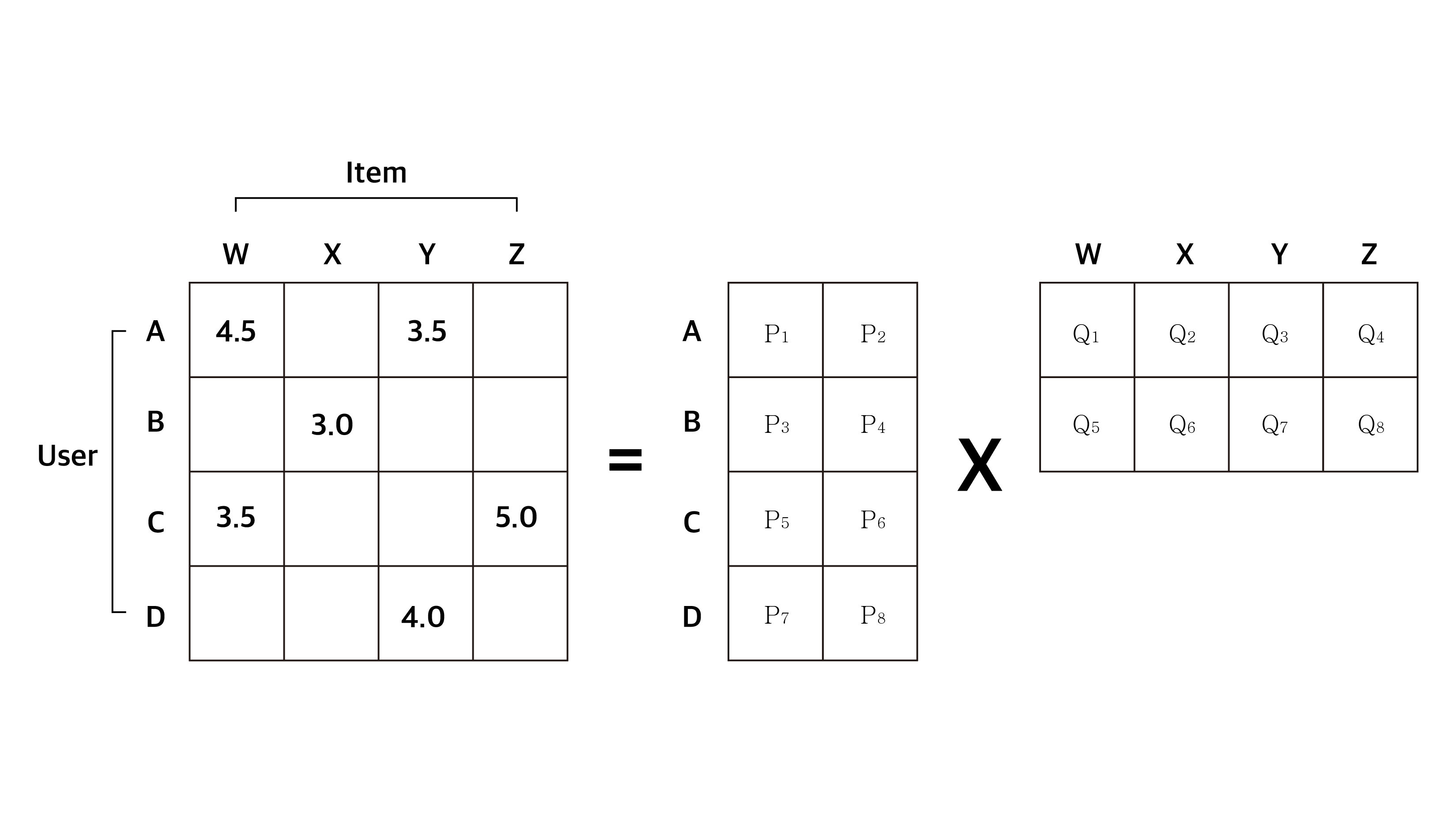
위의 그림처럼 Matrix Factorization, 즉 행렬 분해는 Latent Matrix를 기반으로 이루어집니다. 그리고 그림을 보시면 감이 오시겠지만 Matrix Factorization을 통해 분해된 각 Latent Matrix의 P, Q 가중치를 구해주어야 합니다.

2.1 Matrix Factorization 원리

그럼 지금부터 Matrix Factorization의 원리에 대해 알아보겠습니다. 들어가기에 앞서 사용될 단어를 정의하고 가겠습니다.

latent Factor = Item, User
\(N_f\) = dimension of latent Factor
\(N_i\) = dimension of Item
\(N_u\) = dimension of User

먼저 원래 Matrix를 latent Matrix로 분해하기 위해서는 Latent Factor의 차원이 필요합니다. implicit의 ASL 알고리즘을 보면 default 값이 100으로 설정되어 있지만 40 ~ 200사이로 설정하는 경우도 많습니다. 그렇다면 이제 행렬 분해 그림을 다시 보겠습니다.

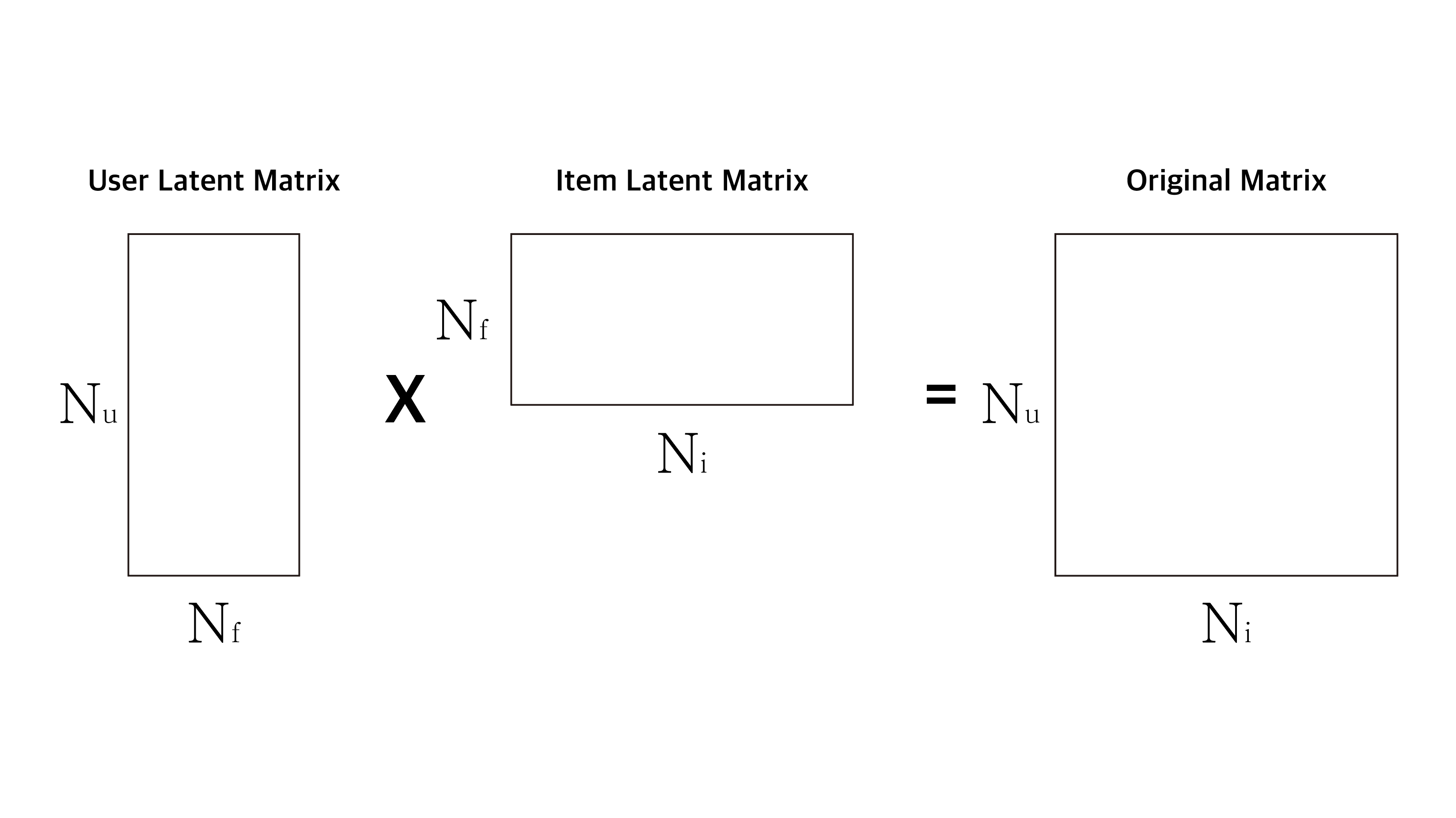
이제는 이 그림이 꽤나 익숙하실 것으로 생각됩니다. 이렇게 위의 그림처럼 행렬분해를 할때 주의해야할 점은 User Latent Matrix 혹은 Item Latent Matrix를 만들 때, 행렬 안의 값을 Original Matrix에서 가져오는 것이 아니라 아주 작은 랜덤 값을 채워넣어 각 Latent Matrix를 초기화 시킵니다. 그럼 이제 어떻게 계산되는지 그림으로 보겠습니다.

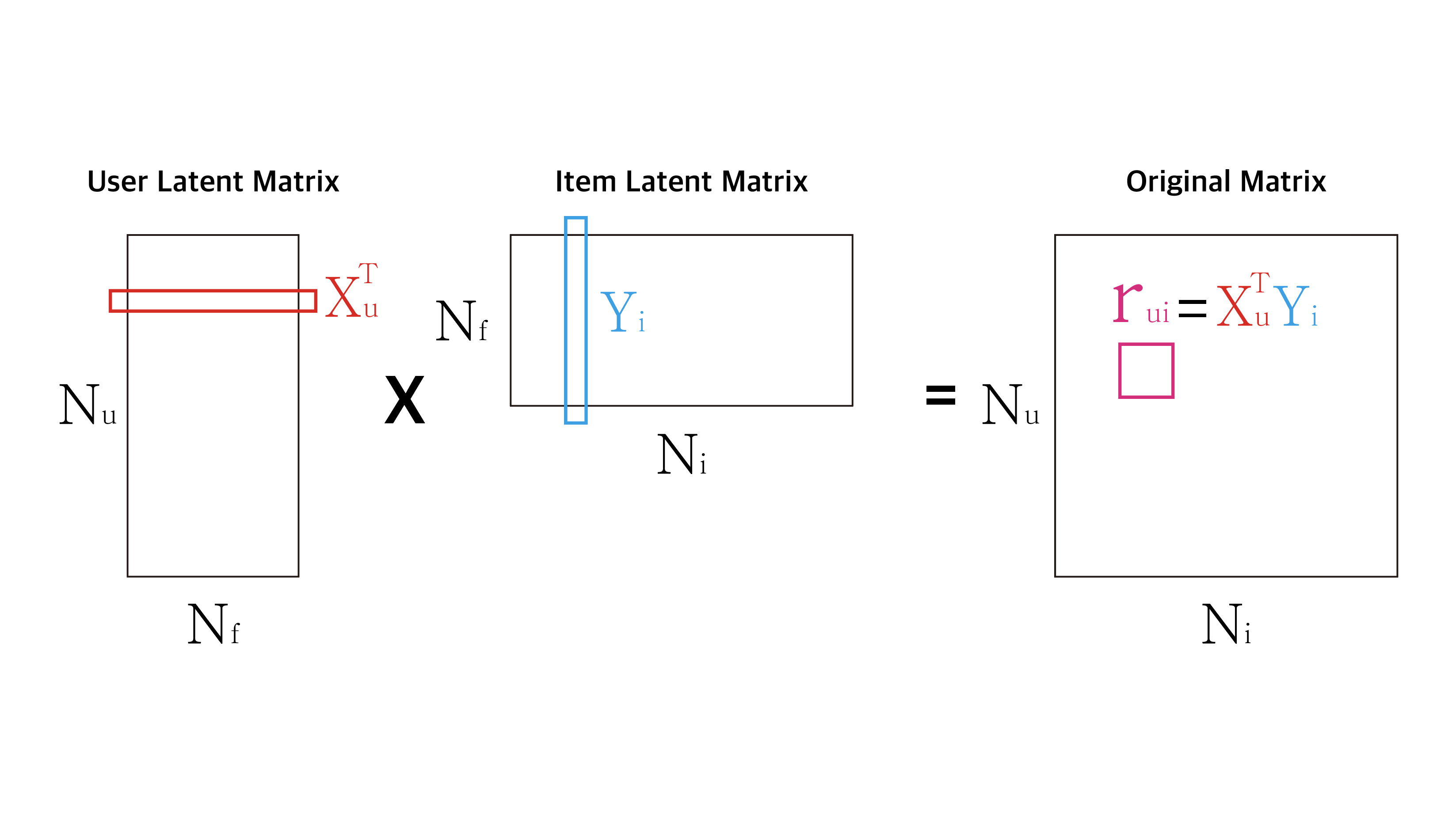
계산 원리는 단순한 행렬 곱으로 매우 간단합니다. 따라서 결론적으로 평점을 잘 예측하기 위해서 \(X_u^T\)와 \(Y_i\)가 잘 예측되어야 한다는 것을 직관적으로 이해할 수 있습니다.

2.2 Matrix Factorization 최적화

그렇다면 어떻게 Latent Matrix 값을 최적화시킬 수 있을까요? 이를 위해 Matrix Factorization의 Loss Function을 보겠습니다.

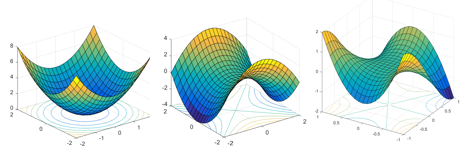
\[L(f) = {min \sum\limits_{u, i}(r_{ui} - x_u^T y_i)^2 + \lambda(\sum\limits_{u}||x_u||^2 + \sum\limits_{i}||y_i||^2)}\]

위의 Loss Function에서 특이한 점은 최적화가 필요한 변수가 하나가 아니라 \(x_u, y_i\)두개라는 것입니다. 그렇기에 loss 함수가 convex형태가 아닌 non-convex형태가 나옵니다.

Convex(맨 왼쪽 그림)와 Nonconvex 그래프

따라서 우리가 흔히 아는 일반적인 Single Neural Network의 Gradient Descent를 사용하면 위의 Loss function이 non-convex 형태이기 때문에 학습이 제대로 안될 수 있습니다. 따라서 Matrix Factiorization에는 Gradient Descent를 위해 ALS(Alternating Least Squares)알고리즘을 사용합니다.

이렇게 이번 포스팅을 통해 Matrix Factorization에 대해 간략하게 알아보았습니다. 잘못된 내용은 댓글로 남겨주시고, 다음 포스팅 에서는 ALS에 대해 자세히 알아보겠습니다.

Matrix Factorization 1편

With Latent Matrix

들어가기

1. Latent Matrix

2. Matrix Factorization

2.1 Matrix Factorization 원리

2.2 Matrix Factorization 최적화

reference

CATALOG

FEATURED TAGS