잘못된 내용은 언제든지 밑의 댓글로 알려주세요!

들어가기

이번 포스팅은 ALS 알고리즘에 대한 포스팅입니다. ALS 알고리즘을 더 쉽게 이해하기 위해 전 포스팅을 한번 보고오시면 좋을것 같습니다. 이번 포스팅은 이 글을 참조하였습니다. 잘못된 내용은 댓글이나 메일로 알려주세요.

1. ALS 알고리즘

ALS 알고리즘의 ‘Alternating’에서 알 수 있듯이 ALS는 행렬 최적화를 위해 \(X_u\)와 \(Y_i\)을 교대로 학습시킵니다. 두 행렬을 한번에 최적화시키는 것이 아닌 \(X_u\)행렬을 최적화 시킬 때에는 \(Y_i\)행렬을 상수로 놓고, \(Y_i\)를 최적화 시킬 때에는 \(X_u\)행렬을 상수로 놓습니다. 그렇기 때문에 ALS 알고리즘에서 편미분은 매우 중요합니다.

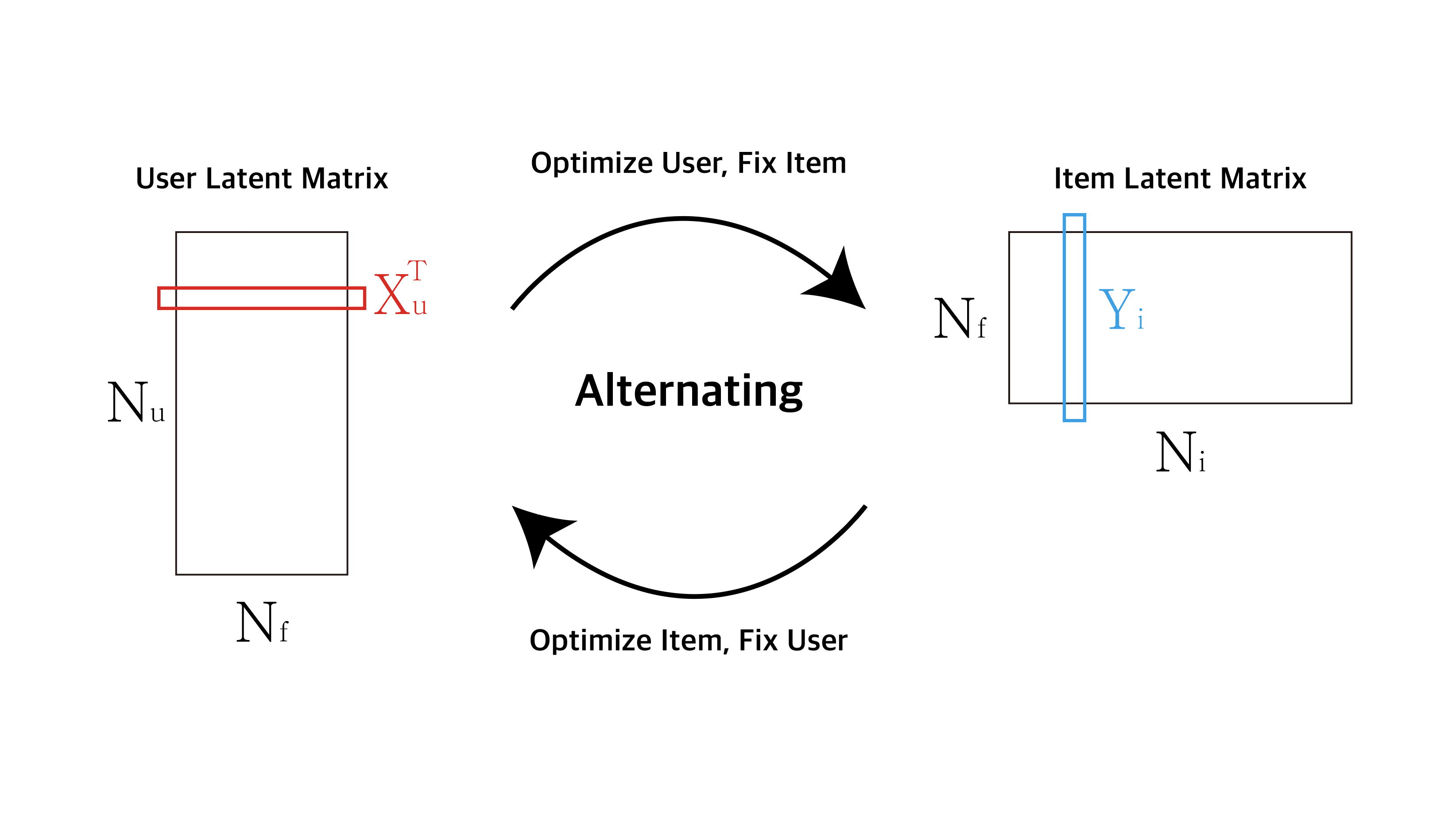
1-1. ALS 알고리즘 계산

이제 ALS를 사용하여 최적의 \(X_u\)행렬과 \(Y_i\)행렬을 찾아보겠습니다. 그런데 ALS에 사용되는 Loss Function은 전에 소개했던 Matrix Factorization의 Loss Function과 조금 다릅니다. 조금 바뀐 Loss Function부터 보겠습니다.

\[L(f) = {min \sum\limits_{u, i}c_{ui}(p_{ui} - x_u^T y_i)^2 + \lambda(\sum\limits_{u}||x_u||^2 + \sum\limits_{i}||y_i||^2)}\]

여기서 새롭게 추가된 것은 \(c_{ui}\)와 \(p_{ui}\)입니다. 그럼 이게 무엇을 의마하는지 다른 파라미터와 함께 살펴보겠습니다.

1-2. ALS 알고리즘 파라미터

ALS 파라미터를 살펴보기 전에 implicit 데이터에 대해 잠깐 이야기하겠습니다. Implicit 데이터는 유저가 간접적으로 선호나 취향을 나타내는 데이터를 말합니다. 예를들어 방문 기록, 머문 시간, 클릭 횟수 등등이 implicit 데이터라고 할 수 있습니다. 그렇기에 implicit 데이터는 다음의 특징이 있습니다.

사용자의 행동만으로도 데이터가 생성되기에 데이터양이 많다.
부정적인 피드백이 없다.
데이터값은 선호와 비선호를 나타내는 것이 아니다.
데이터값에 잡음(noise)가 많다.

예를들어 이야기하면 유저가 홈페이지를 들어가는 것만으로도 데이터가 생성되고, 어떤 유저가 특정 상품을 많이 클릭했다하더라도 유저가 해당 상품을 선호한다고 확실히 말할 수 없습니다. 이런 이유로 데이터 해석에 많은 잡음이 발생합니다.

그렇다면 제가 왜 갑자기 수식을 설명하다 말고 implicit 데이터를 설명했을까요? 그 이유는 바로 이런 이유 때문에 \(c_{ui}\)와 \(p_{ui}\)가 추가되었기 때문입니다. 이제 \(c_{ui}\)와 \(p_{ui}\)의 수식을 살펴보겠습니다. 먼저 \(p_{ui}\)입니다.

\[p_{ui} = {1 \;\;\; if \; (r_{ui} > 0)}\]
\[p_{ui} = {0 \;\;\; if \; (r_{ui} = 0)}\]

앞서 Implicit 데이터값은 선호, 비선호를 나누는게 아니라고 말씀드렸습니다. 따라서 단순히 \(r_{ui}\)값이 있으면 1, 없으면 0으로 변환시켜줍니다. 이런 binary 치환을 통해 값이 없는 \(r_{ui}\)데이터에도 0을 넣어주어, 모델 학습 시 모든 데이터를 사용할 수 있게 됩니다. (치환된 \(p_{ui}\)는 선호\((=1)\)와 비선호\((=0)\)를 의미합니다.)

그런데 여기서 문제가 발생합니다. 그 문제는 바로 \(r_{ui}\)가 0이라고 해서 user가 이 item에 관심이 없다고 말할 수 없기 때문입니다. 예를 들어 제가 어떤 상품에 매우 관심이 있었지만 일시적인 홈페이지 장애 때문에 해당 상품을 클릭하지 못했다고 가정해봅시다. 그럼 \(r_{ui}\)값이 Null이여서 \(p_{ui}\)값이 0으로 바뀝니다. 그러나 저는 이 아이템에 매우 관심이 있었기에 0으로 치환된 \(p_{ui}\)값은 신뢰도가 낮다고 할 수 있습니다.

따라서 이런 문제를 방지하기 위해 \(p_{ui}\)의 신뢰도 레벨을 평가할 수 있는 \(c_{ui}\)값이 곱해지는 것입니다. 그렇다면 이제 \(c_{ui}\)의 수식을 살펴보겠습니다.

\[c_{ui} = {1 + \alpha r_{ui}}\]

여기서 \(\alpha\)는 사용자 정의 hyper parameter를 의미합니다. 자 그럼 이제 차례대로 정리해보겠습니다.

데이터의 선호와 비선호의 차이가 어느정도 있다고 판단될 때

\(r_{ui}\)값이 있으면 선호, 없으면 비선호로 가정할 수 있다.
가정에 의해 평점이 존재하면 실제로 선호하는 것이고 이때, 신뢰도가 높다고 평가할 수 있다.
신뢰도가 높으니 신뢰도 레벨을 평가할 수 있는 \(c_{ui}\)값을 크게해야 한다.
\(c_{ui}\)값을 크게 하기 위해 \(\alpha\)값을 크게 설정한다.
커진 \(\alpha\)로 인해 \(r_{ui}\)값이 있는 \(c_{ui}\)와 없는 \(c_{ui}\)의 차이가 커진다.
\(c_{ui}(p_{ui} - x_u^T y_i)^2\) 공식으로 인해 \(p_{ui}\)값이 0인 것과 1인 것의 차이가 커진다.(\(x_u^T y_i\)는 동일)
0일때, 1일때 값의 차이가 크므로 이는 binary로 구분된다.
binary로 구분되기 때문에 선호와 비선호로 가정한것은 어느정도 타당하다.

이처럼 1번의 가정과 8번의 결론이 비슷하기 때문에 데이터의 선호와 비선호가 어느정도 구분될 수 있다고 생각되면 \(\alpha\)값을 크게, 아니라면 \(\alpha\)값을 작게 설정해야 합니다. 이제 이걸 그림 하나로 보여드리겠습니다.

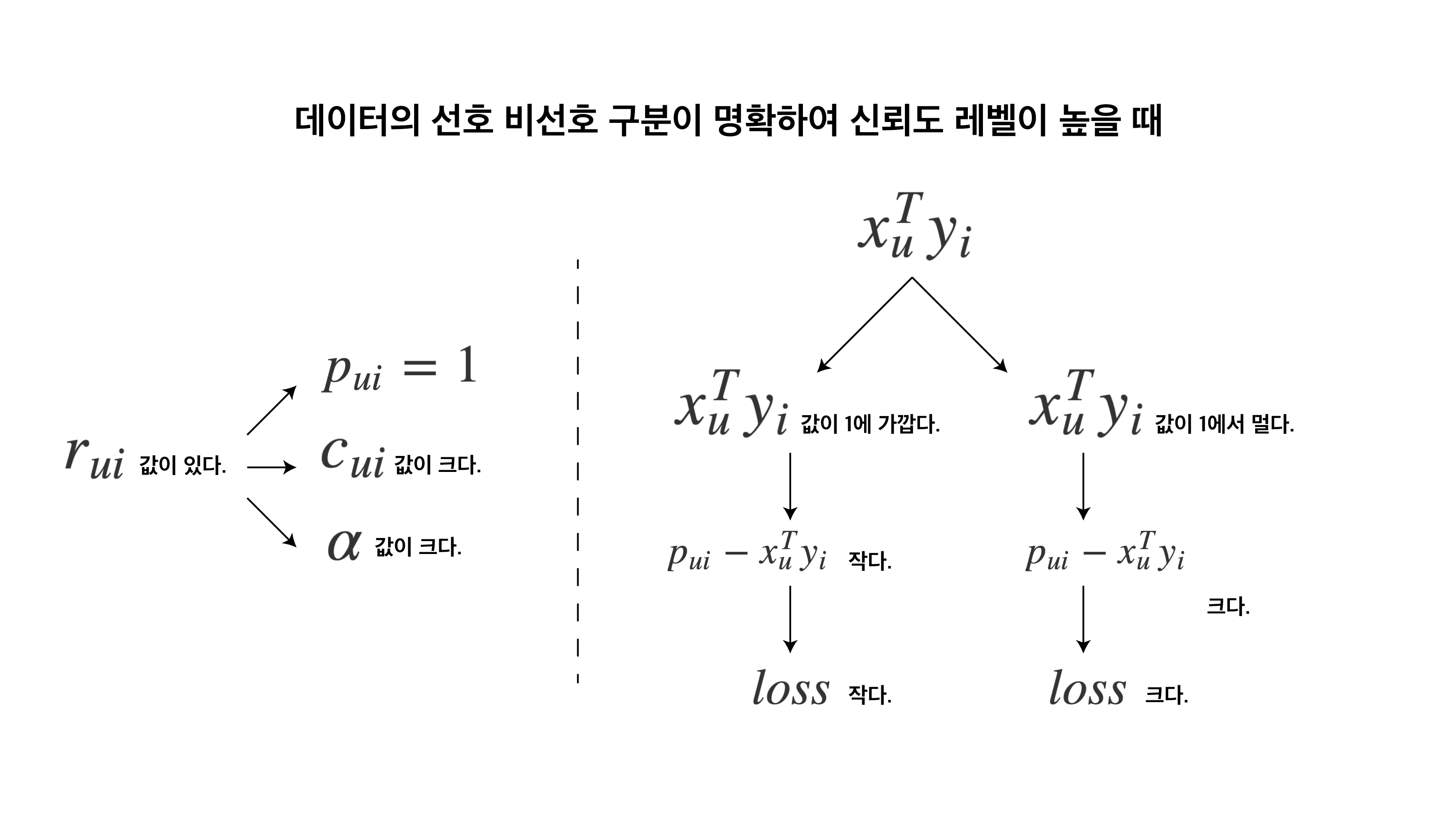
따라서 위 그림처럼 신뢰도 레벨이 높을 때 잘못 예측하면 커진 \(c_{ui}\)값만큼 loss가 더 커지는 효과가 있습니다. 쉽게 말하면 신뢰도가 높다고 했는데 잘못 예측하니 모델이 더 큰 벌을 받는다고 생각하시면 될것 같습니다.

마지막으로 \(\lambda\)에 대해서 살펴보겠습니다. 이 부분은 L2 Reguralization과 같은 원리입니다. 위에서 \(\alpha\)값이 커지면 \(c_{ui}\)와 \(p_{ui}\)가 같이 커지게 되는데 이러면 가중치가 한쪽으로 쏠리게 됩니다. 따라서 \(\lambda\)라는 regualization parameter를 추가하여 가중치가 한쪽으로 너무 쏠리지 않게끔 해줍니다.

이제 ALS Loss Function의 대략적인 파라미터와 원리 설명은 끝난것 같습니다. 이 부분에 제 주관적인 설명이 어느정도 포함되어 있어 오류가 있다면 꼭 댓글로 알려주세요. 그럼 이제 편미분을 통한 최적값을 찾아보도록 하겠습니다.

1-3. ALS 알고리즘 계산

이제 ALS 알고리즘을 계산해보겠습니다. 알고리즘을 계산하기에 앞서 사용된 표기의 정의를 알아보겠습니다.

1-3-1. 표기 정의

\(N_u\) : Number of Users
\(N_i\) : Number of Items
\(N_f\) : Dimension of Latent Factor
\(X\) : User Latent Factor Matrix, \(shape = (N_f, N_u)\)
\(x_u\) : User Latent Vector of Specific index u
\(Y\) : Item Latent Factor Matrix \(shape = (N_f, N_i\))
\(y_i\) : Item Latent Vector of Specific index i

1-3-2. ALS 알고리즘 계산 과정

\(x\)에 대해 편미분을 수행해줍니다.

\[\displaystyle \frac{\triangle L(X_u)}{\triangle X_u} = {-2\sum\limits_{u, i}C_{ui}(p_{ui} - x_U^T y_i)Y_i + 2 \lambda x_u}\]

Gradient Descent 원리와 마찬가지로 위 식의 좌변이 0이 되어야 합니다.

\[0 = {-2\sum\limits_{u, i}C_{ui}(p_{ui} - x_u^T y_i)y_i + 2 \lambda x_u}\]

시그마를 분해 한 후 좌변과 우변을 정리합니다.

\[{\sum\limits_{i}C_{ui}(x_u^T y_i)Y_i + \lambda x_u} = {\sum\limits_{i}C_{ui}(p_{ui})}y_i\]

전개를 위해 행렬의 순서를 바꿔줍니다.

위에서 \(C_{ui}\). \(X_u^T Y_i\), \(Y_i\) 모두 스칼라입니다. 여기서 전개를 위해 \(X_u^T Y_i\)항을 전치하겠습니다. 스칼라이기에 전치해도 결과값은 변하지 않습니다.

\[{\sum\limits_{i}C_{ui}y_i(y_i^T x_u) + \lambda x_u} = {\sum\limits_{i}C_{ui}(p_{ui})}y_i\]

다시 항을 정리해줍니다.

\[{(\sum\limits_{i}C_{ui}y_i y_i^T + \lambda I)x_u} = {\sum\limits_{i}C_{ui}(p_{ui})}y_i\]

여기서 잠깐 \(\sum\limits_{i}C_{ui}y_i y_i^T\)의 전개 형태를 살펴보겠습니다.

\[\sum\limits_{i}C_{ui}y_i y_i^T = {C_{u1}y_1 y_1^T + C_{u2}y_2 y_2^T + C_{u3}y_3 y_3^T + + \cdots}\]

그렇다면 위 식은 다음의 행렬로 나타낼 수 있을 것입니다.

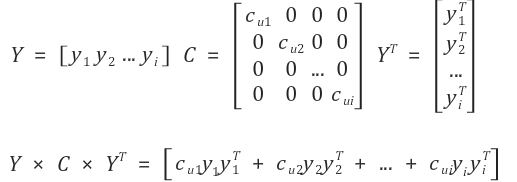
우변도 똑같은 방식으로 시그마를 풀어줄 수 있습니다. 그럼 다음의 식을 얻게 됩니다.

\[{(Y C_{u} Y^T + \lambda I)x_u} = Y^T C_{u} p(u)\]

최적화된 \(X_u\)를 찾기 위해 역행렬을 곱해줍니다.

\[x_u = (Y C^u Y^T + \lambda I)^{-1} Y^T C^u p(u)\]

좌변의 스칼라값인 \(Y C^u Y^T\)를 전치해줍니다. 스칼라이기에 전치해도 똑같습니다.

\[x_u = (Y^T C^u Y + \lambda I)^{-1} Y^T C^u p(u)\]

위 식을 통해 Loss의 미분 값이 0이 되도록 하는 \(x_u\)값을 찾았습니다. 이제 같은 방식으로 \(y_i\)값을 찾으면 다음과 같습니다.

\[y_i = (X^T C^i X + \lambda I)^{-1} X^T C^i p(u)\]

따라서 위처럼 최적화 \(x_u\)를 찾을 때에는 \(y_i\)를 고정해놓고, 반대로 최적화 \(y_i\)를 찾을 때에는 \(x_u\)를 고정해두는 것이 ALS 알고리즘의 핵심입니다.

이제 다음 포스팅을 통해 ALS 알고리즘을 직접 구현해보겠습니다.

Matrix Factorization 2편

With ALS 알고리즘