잘못된 내용은 언제든지 밑의 댓글로 알려주세요!

들어가기

이번 포스팅에서는 Matrix Factorization에 사용되는 ALS 알고리즘을 직접 구현해보겠습니다. 이번 포스팅은 이 글을 참조하였습니다. 잘못된 내용은 댓글이나 메일로 알려주세요.

1. ALS 공식 내 필요한 Hyper Parameters

앞선 포스팅에서 ALS 공식 전개를 위한 최종 결과식을 살펴보겠습니다.

\[x_u = (Y^T C^u Y + \lambda I)^{-1} Y^T C^u p(u)\] \[y_i = (X^T C^i X + \lambda I)^{-1} X^T C^i p(u)\]

여기서 사용자 Hyper Parameter가 필요한 공식은 다음과 같습니다.

위의 식 \(x_u, y_i\)에서 \(\lambda\)
\(c_{ui} = {1 + \alpha r_{ui}}\)에서 \(\alpha\)
\(X \; shape = (N_f, N_u)\)와 \(Y \; shape = (N_f, N_i)\)에서 \(N_f\)

따라서 알고리즘을 구현하기 전에 위의 Hyper Parameter를 지정해 주어야 합니다. 저는 원작자분께서 정해놓은 파라미터를 그대로 가져가겠습니다.

r_lambda = 40
nf = 200
alpha = 40

2. ALS 파이썬 코드 구현

그럼 지금부터 파이썬 코드를 살펴보겠습니다.

2-1. 예측용 더미변수 생성

먼저 예측을 위한 가상의 더미 변수를 행렬로 생성해주겠습니다.

shape = (10, 11)
\(N_u : 10\) => Number of Users
\(N_i : 11\) => Number of Items

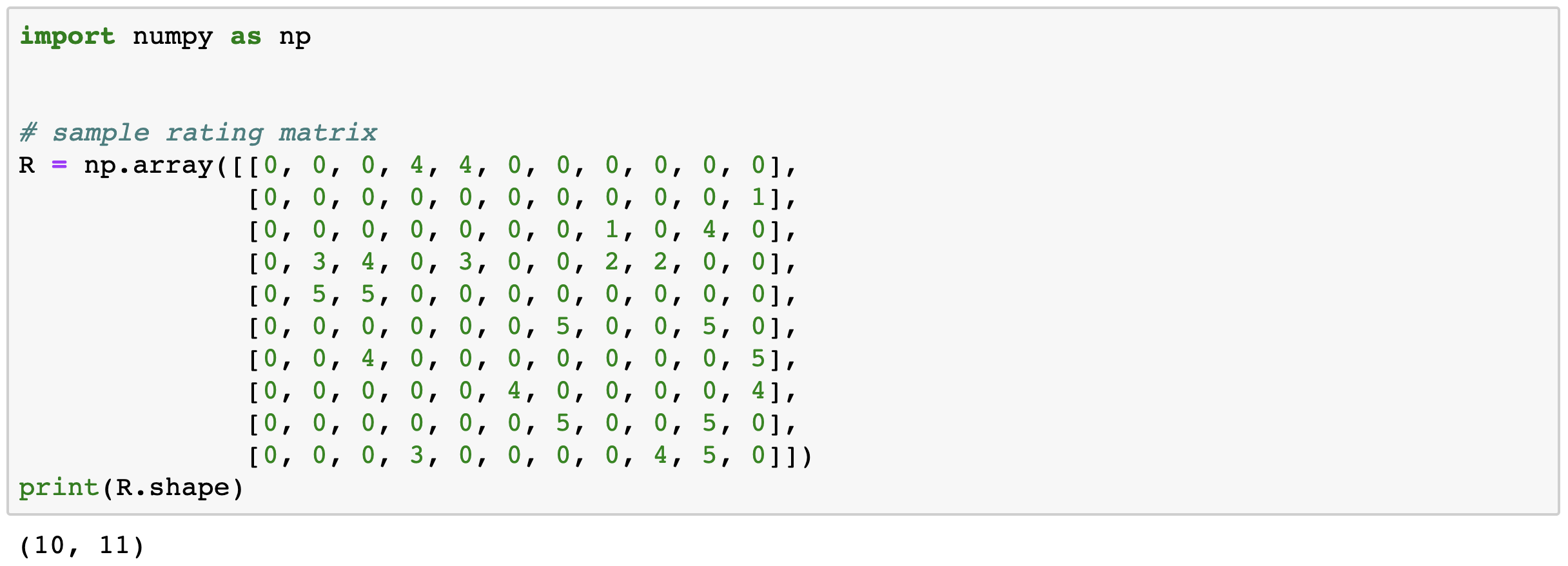
위 행렬에서는 모든 값들이 채워져있지만 실제로 0은 Null값이라고 생각하고 봐주시는게 더 좋습니다.

2-2. Latent Matrix 생성

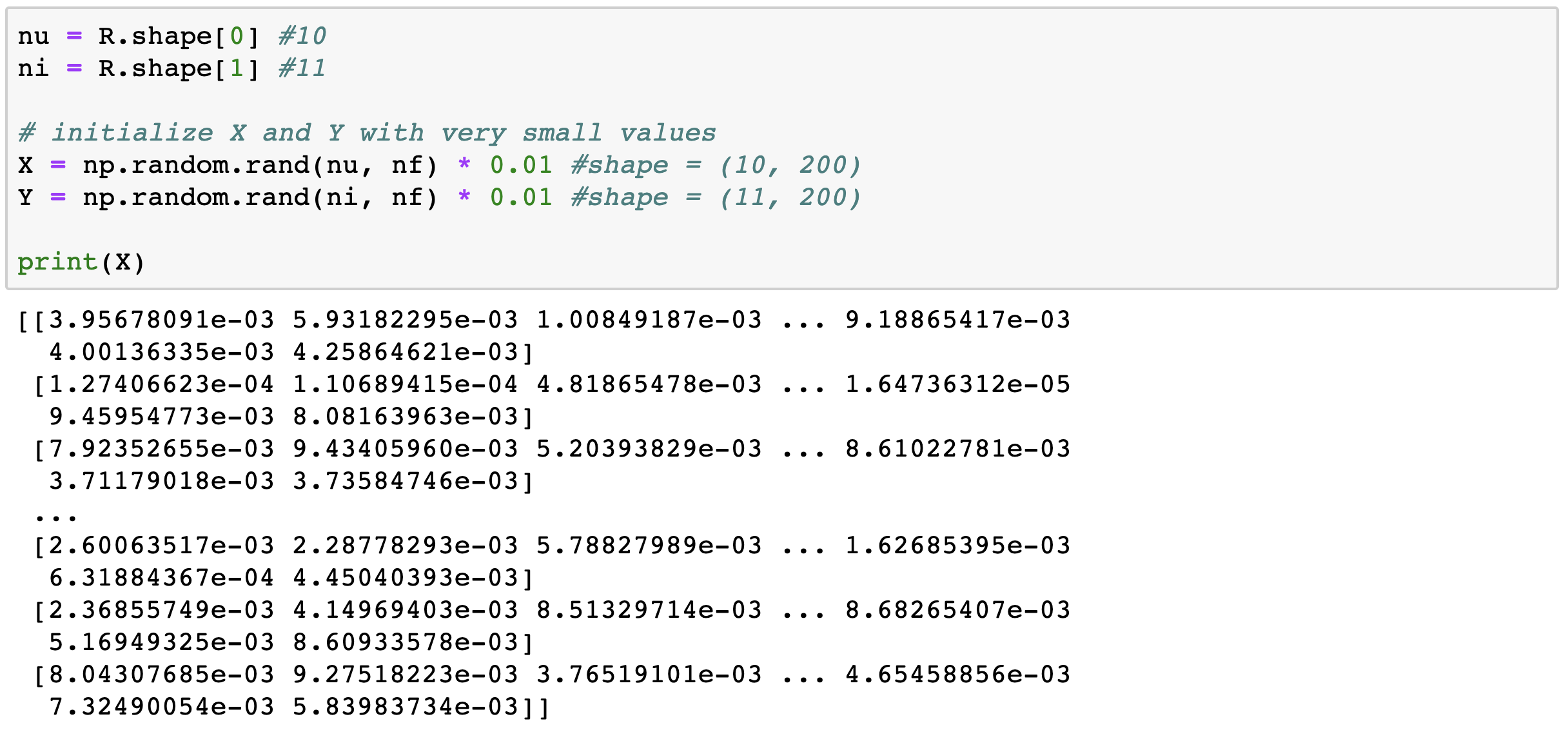
\(N_f : 200\) => Latent Matrix의 차원

이제 (10, 11)차원의 행렬을 분해하여 두개의 Latent Matrix을 만들어야 합니다. Latent Matrix의 차원 중 하나는 hyper parameter인 \(N_f\)로 지정해줍니다. 또한 Latent Matrix의 행렬 값들은 분해 전 행렬에서 온 것이 아닌 아주 작은 값으로 초기화된 값입니다.

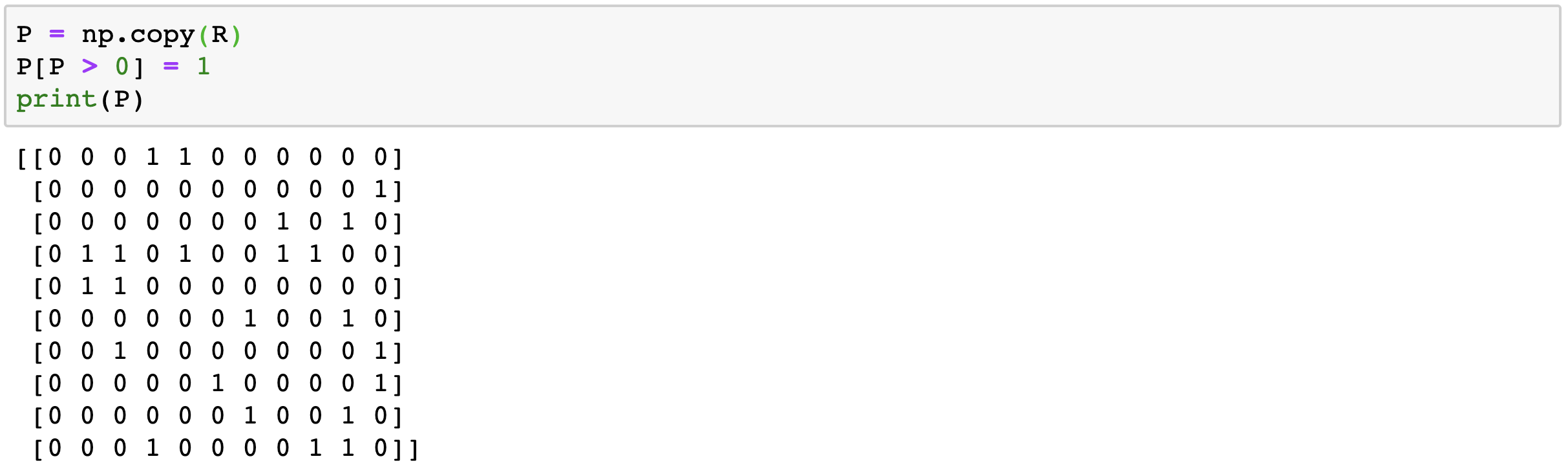
2-3. Binary Matrix P 설정

앞서서 implict 데이터는 값이 없는 데이터도 전부 사용한다고 말한바 있습니다. 그렇기에 Binary로 행렬값이 있으면 1, 없으면 0으로 치환해주어야 합니다.

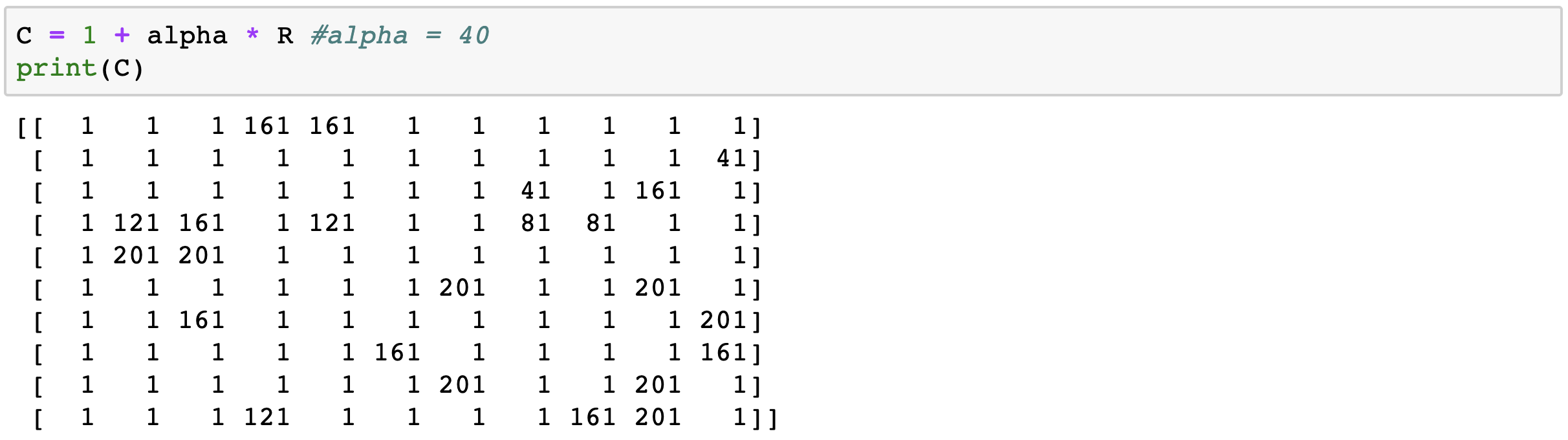
2-4. 신뢰도 행렬 C 설정

\(c_{ui} = {1 + \alpha r_{ui}}\)는 \(c_{ui}\)는 Binary Matrix P의 신뢰도 레벨을 평가할 수 있는 값입니다. \(c_{ui}\)행렬을 만들기 위해 Hyper Parameter \(\alpha\)값을 지정해주어야 합니다.

2-5. Loss Function 구현

이제 학습을 위해 Loss Function을 구현해야 합니다. 구현에 앞서 Loss Function 공식을 다시 보고 가겠습니다.

\[L(f) = {min \sum\limits_{u, i}c_{ui}(p_{ui} - x_u^T y_i)^2 + \lambda(\sum\limits_{u}||x_u||^2 + \sum\limits_{i}||y_i||^2)}\]

코드 구현을 위해 위 공식을 세 가지 부분과 \(\lambda\)정규화 부분으로 나누어줍니다.

Predict Error : \((p_{ui} - x_u^T y_i)^2\)
Confidence Error : \(c_{ui}(p_{ui} - x_u^T y_i)^2\)
Total Loss : Predict Error + Confidence Error

2-5. Optimizer 구현

이제 Loss을 위한 Optimizer를 구현해야 합니다. ALS 편미분을 얻은 Optimizer를 살펴보면 다음과 같습니다.

\[x_u = (Y^T C^u Y + \lambda I)^{-1} Y^T C^u p(u)\] \[y_i = (X^T C^i X + \lambda I)^{-1} X^T C^i p(u)\]

제 포스팅을 쭉 보셨다면 이제 위 공식이 꽤 눈에 익었으리라 생각합니다. 그럼 이제 위 식을 구현해보면 다음과 같습니다. 주석에 달린 차원과 위 공식을 함께 보시면 이해하기 어렵지 않을 것입니다.

2-6. 학습 구현

이제 위에서 구현한 Optimizer를 가지고 학습을 진행해보겠습니다. ALS 학습에서는 ‘번갈아’가 핵심입니다.

위의 코드처럼 2의 배수일때와 2수 배수가 아닐 때 학습을 다르게 해야 정규화가 잘 진행되어 학습이 더 잘됩니다.

이제 최종적으로 학습 결과를 보시겠습니다.

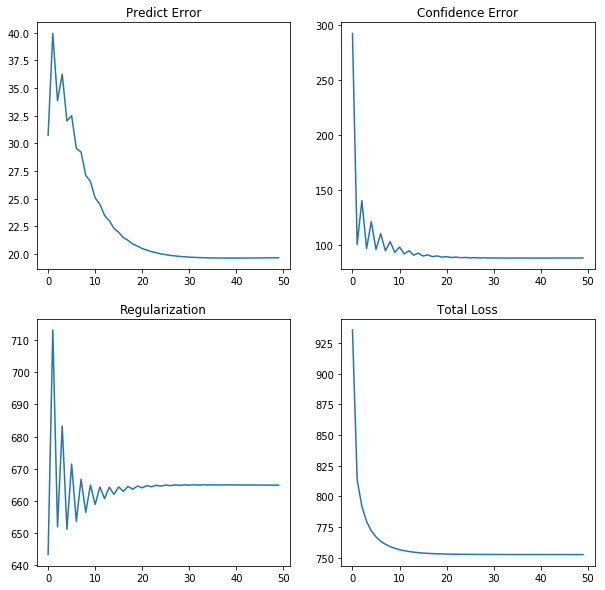
여기서 에러가 낮아짐과 동시에 Regularization이 안정적으로 수행되고 있음을 볼 수 있습니다.

또한 여기서 Total Loss가 일정수준 이하로 떨어지지 않는 이유는 implicit 데이터셋 특성상 값이 없는 데이터에도 값을 넣어주어 예측하기 때문에 값이 없는 부분에서 무조건적으로 에러가 발생할 수밖에 없습니다. 이제 예측값과 실제값을 살펴보겠습니다.

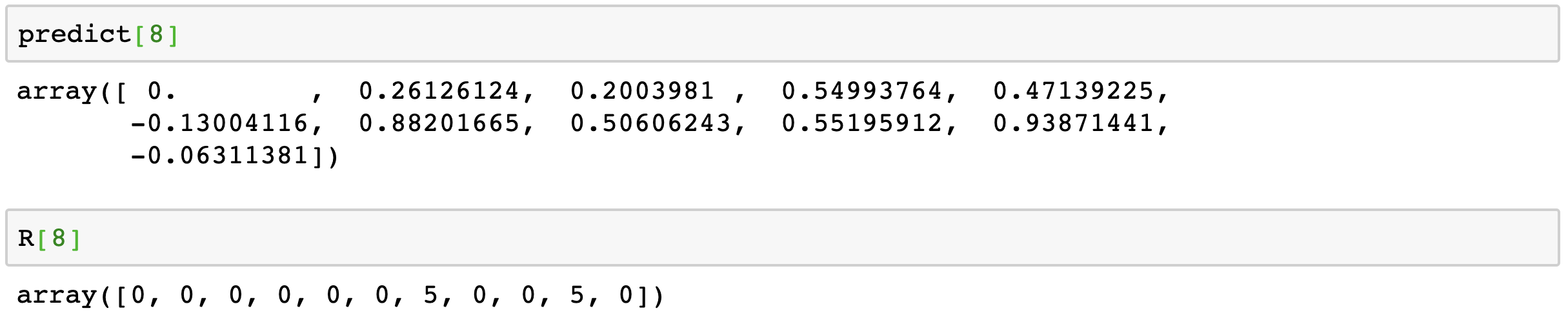
위 그림을 보시면 실제로 값이 있는 부분에 예측값이 더 큰 값을 매핑했음을 알 수 있습니다.

이렇게 ALS 알고리즘을 직접 구현하는 작업은 끝났습니다. 다음 포스팅에서는 implicit의 ALS함수를 사용하여 ALS 알고리즘을 사용해보겠습니다.

전체코드

# Hyper Parameter Setting
r_lambda = 40
nf = 200
alpha = 40

import numpy as np


# sample rating matrix
R = np.array([[0, 0, 0, 4, 4, 0, 0, 0, 0, 0, 0],
              [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
              [0, 0, 0, 0, 0, 0, 0, 1, 0, 4, 0],
              [0, 3, 4, 0, 3, 0, 0, 2, 2, 0, 0],
              [0, 5, 5, 0, 0, 0, 0, 0, 0, 0, 0],
              [0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
              [0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 5],
              [0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 4],
              [0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
              [0, 0, 0, 3, 0, 0, 0, 0, 4, 5, 0]])

nu = R.shape[0] #10
ni = R.shape[1] #11

# initialize X and Y with very small values
X = np.random.rand(nu, nf) * 0.01 #shape = (10, 200)
Y = np.random.rand(ni, nf) * 0.01 #shape = (11, 200)

P = np.copy(R)
P[P > 0] = 1
C = 1 + alpha * R #alpha = 40

# Define Loss Function
def loss_function(C, P, xTy, X, Y, r_lambda):
    predict_error = np.square(P - xTy)
    confidence_error = np.sum(C * predict_error)
    regularization = r_lambda * (np.sum(np.square(X)) + np.sum(np.square(Y)))
    total_loss = confidence_error + regularization
    return np.sum(predict_error), confidence_error, regularization, total_loss

# Define User Opimizer Function
def optimize_user(X, Y, C, P, nu, nf, r_lambda):
    # Y = number of Items, shape = (11, 200)
    yT = np.transpose(Y) #shape = (200, 11)
    for u in range(nu):
        Cu = np.diag(C[u]) #shape = (11, 11)
        yT_Cu_y = np.matmul(np.matmul(yT, Cu), Y) #{(200, 11)*(11, 11)}*(11, 200) = (200, 200)
        lI = np.dot(r_lambda, np.identity(nf))
        yT_Cu_pu = np.matmul(np.matmul(yT, Cu), P[u])
        X[u] = np.linalg.solve(yT_Cu_y + lI, yT_Cu_pu)

# Define Item Opimizer Function
def optimize_item(X, Y, C, P, ni, nf, r_lambda):
    # X = number of users, shape = (10, 200)
    xT = np.transpose(X) #shape = (200, 10)
    for i in range(ni):
        Ci = np.diag(C[:, i]) #shape = (10, 10)
        xT_Ci_x = np.matmul(np.matmul(xT, Ci), X) #{(200, 11)*(11, 11)}*(11, 200) = (200, 200)
        lI = np.dot(r_lambda, np.identity(nf))
        xT_Ci_pi = np.matmul(np.matmul(xT, Ci), P[:, i])
        Y[i] = np.linalg.solve(xT_Ci_x + lI, xT_Ci_pi)

# Run Learning
predict_errors = []
confidence_errors = []
regularization_list = []
total_losses = []

for i in range(50):
    if i%2 == 0:   
        optimize_user(X, Y, C, P, nu, nf, r_lambda)
        optimize_item(X, Y, C, P, ni, nf, r_lambda)
    else:
        optimize_item(X, Y, C, P, ni, nf, r_lambda)
        optimize_user(X, Y, C, P, nu, nf, r_lambda)
        
    predict = np.matmul(X, np.transpose(Y))
    predict_error, confidence_error, regularization, total_loss = 
    loss_function(C, P, predict, X, Y, r_lambda)
    
    predict_errors.append(predict_error)
    confidence_errors.append(confidence_error)
    regularization_list.append(regularization)
    total_losses.append(total_loss)

# Make Result Graph
from matplotlib import pyplot as plt
%matplotlib inline

plt.subplots_adjust(wspace=100.0, hspace=20.0)
fig = plt.figure()
fig.set_figheight(10)
fig.set_figwidth(10)
predict_error_line = fig.add_subplot(2, 2, 1)
confidence_error_line = fig.add_subplot(2, 2, 2)
regularization_error_line = fig.add_subplot(2, 2, 3)
total_loss_line = fig.add_subplot(2, 2, 4)

predict_error_line.set_title("Predict Error") 
predict_error_line.plot(predict_errors)

confidence_error_line.set_title("Confidence Error")
confidence_error_line.plot(confidence_errors)

regularization_error_line.set_title("Regularization")
regularization_error_line.plot(regularization_list)

total_loss_line.set_title("Total Loss")
total_loss_line.plot(total_losses)
plt.show()

끝으로 정말 좋은 자료 남겨주신 형준킴님께 감사를 표합니다.

Matrix Factorization 3편

With ALS 알고리즘 코드 구현