들어가기
3편과 4편에서 오프라인 카드소비 데이터와 온라인 물류건수 데이터를 이용해 자판기 업종을 선정하는 과정을 소개했다. 결과적으로 코로나로 인해 오프라인 타격이 제일 심하고 온라인 성장이 제일 더딘 ‘패션 산업’이 선정되었다.
우리팀은 자판기에 뉴노멀 서비스 아이디어를 입혀 패션 산업의 회복탄력성 및 지속가능한 성장을 돕는 아이디어를 제시할 것이다. 근데 이 자판기를 어디에 설치해야 좋을까?
1. 자판기를 어디에 위치시키면 좋을까?
먼저 우리팀은 앞서 최신 뉴노멀 서비스 트렌드로 ‘체험형 오프라인 매장’, ‘중고거래 서비스’, ‘비대면 서비스’를 뽑았다. 그렇다면 이런 트렌드를 잘 반영하기 위해서는 무엇이 중요할까?
코로나 이후 가장 핫한 앱인 ‘당근마켓’의 김재현 대표는 사람들끼리 정보거래를 활발히 하도록 만들기 위해서 반경 6km 내 사람들의 연결에 집중했다고 한다. 따라서 오프라인에 설치된 자판기가 사람들과 연결되고 제 기능을 발휘하기 위해서는 ‘접근성’이 가장 중요한 가치임을 알 수 있다. 이를 위해 우리팀은 MCLP 모델링을 사용하여 접근성을 최대화 할 수 있는 자판기 입지 선정을 진행했다.
2. MCLP 모델링
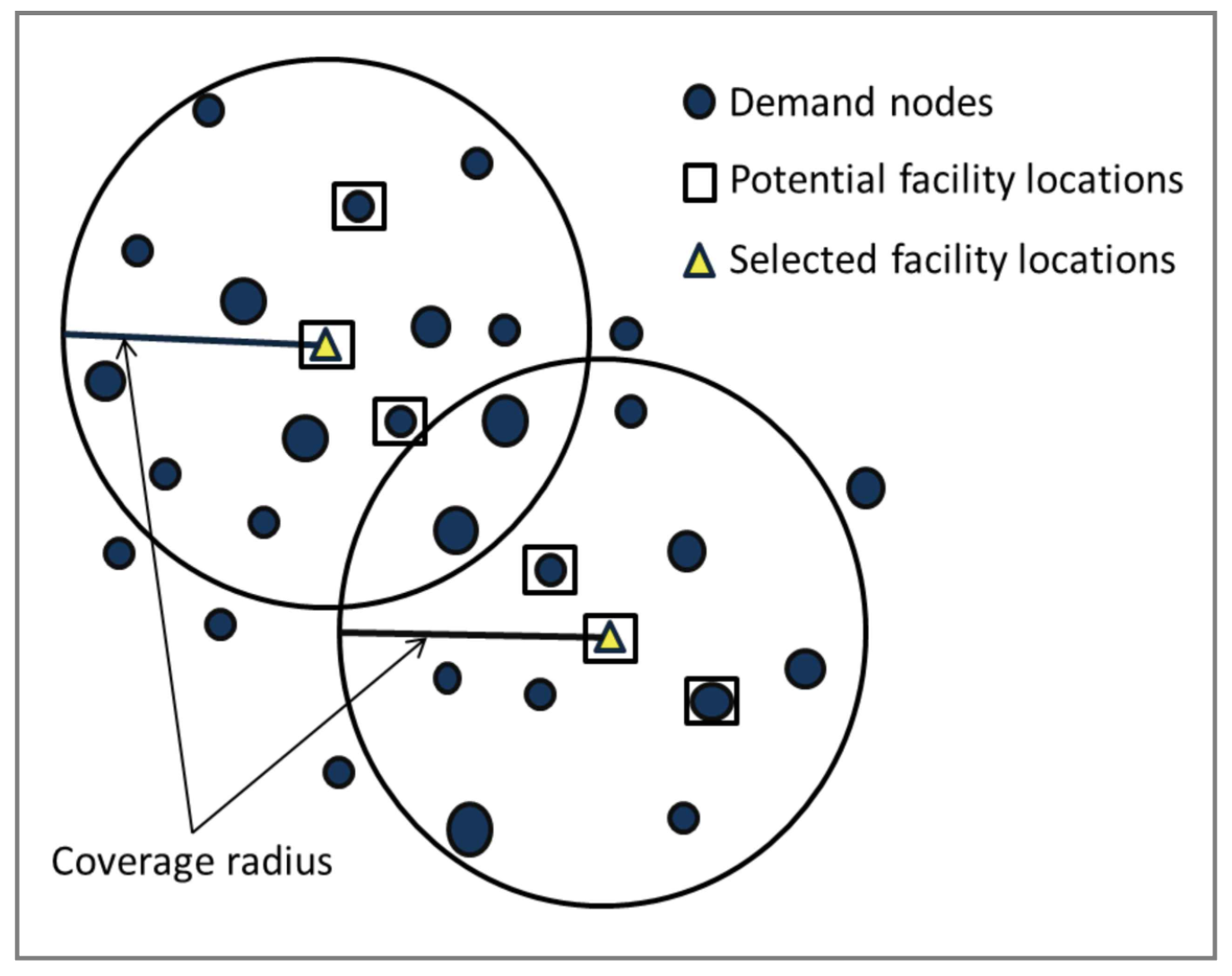
MCLP(Maximal Covering Location Problems)는 최대커버링 모델을 일컫는 말로써, 제한된 시설물의 개수로 지역 수요를 최대한 커버할 수 있는지 파악하기 위한 입지 선정 모델링 방법이다.
| 기존 MCLP 모델링 | 새로운 MCLP 모델링 |
|---|---|
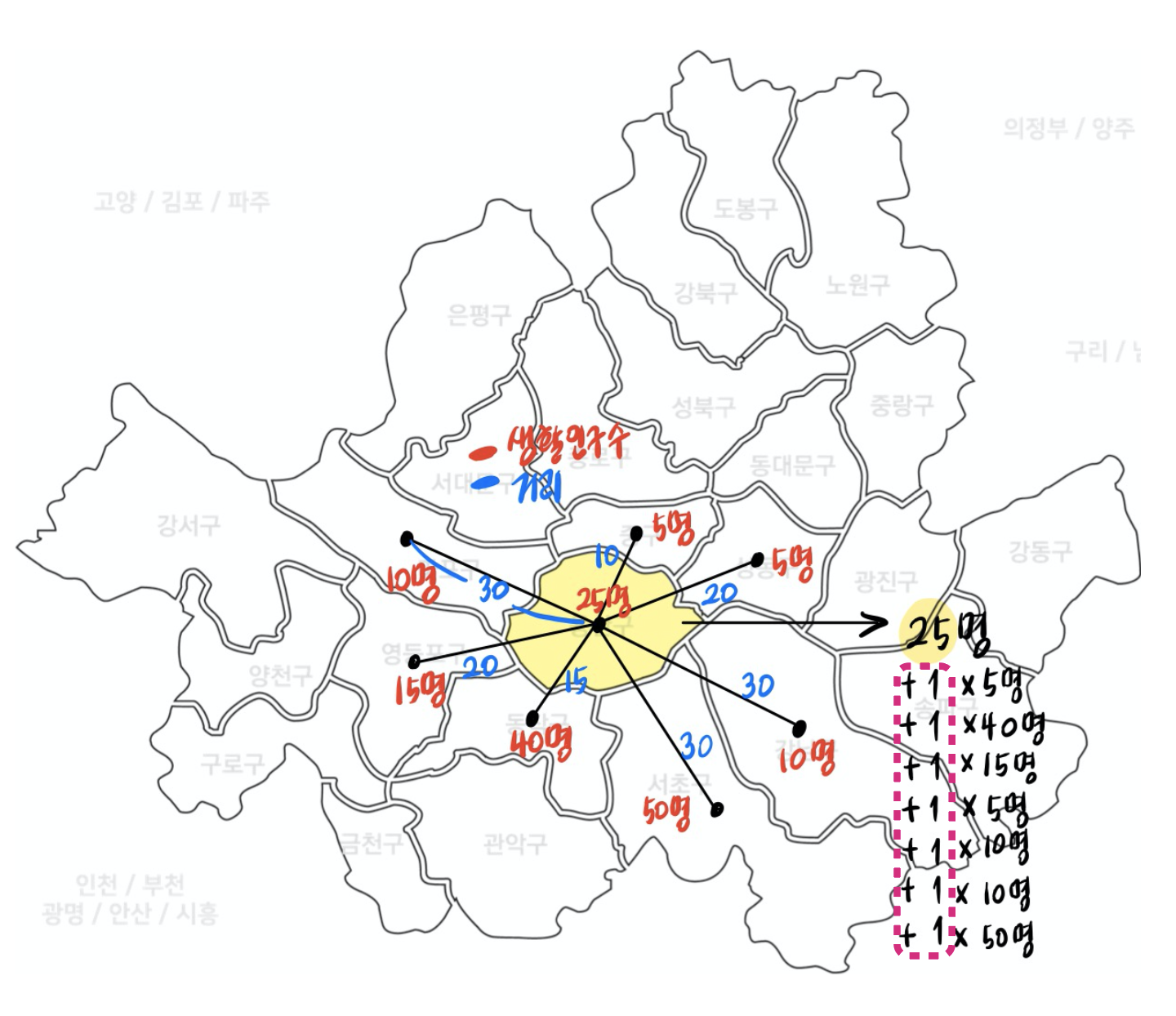 |
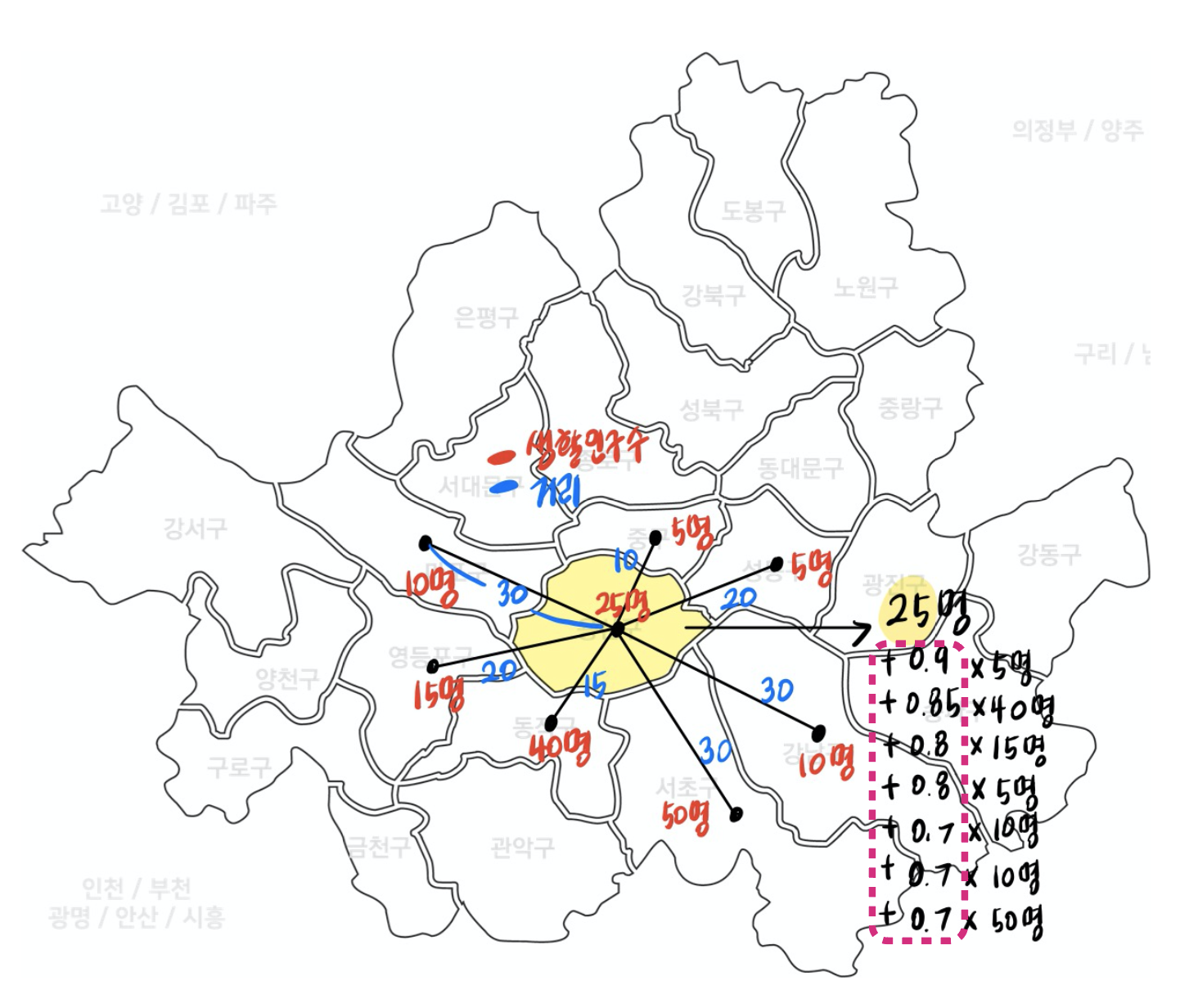 |
그러나 기존 MCLP 모델링은 거리에 상관없이 동일한 가중치르 준다. 그러나 우리팀은 거리에 따라 가중치를 주는 모델로써 기존 MCLP 모델링과 차별화를 두었다. 또한 기존 MCLP 알고리즘에 코로나 기간, 주중/주말 생활인구, 교통편의성과 같은 변수들을 추가하여 코로나 이후의 한국 상황에 더 적합하도록 MCLP 모델을 개선시켰다.
-
MCLP 수식(목적함수) \(= \sum_{p \Subset P}weight_p * (day_{weight_1} * C_{i, j} \circ W_{i, j} \circ {L_{i, 1}}^{(1)} + day_{weight_2} * C_{i, j} \circ W_{i, j} \circ {L_{i, 1}}^{(2)})\)
- \(i, j\) : 행정동
- \(p\) : 코로나 단계별 기간
- \({L_{i, 1}}^{(1)}\) : \(i\)행정동의 코로나 단게별 주중 생활인구
- \({L_{i, 1}}^{(2)}\) : \(i\)행정동의 코로나 단게별 주말 생활인구
- \(C_{i, j}\) : \(i\)행정동가 \(j\)행정동 사이의 교통편의성
- \(W_{i, j}\) : \(i\)행정동가 \(j\)행정동 사이의 거리 가중치
3. MCLP 모델링 적용 과정
MCLP 모델 적용 과정은 어떻게될까?
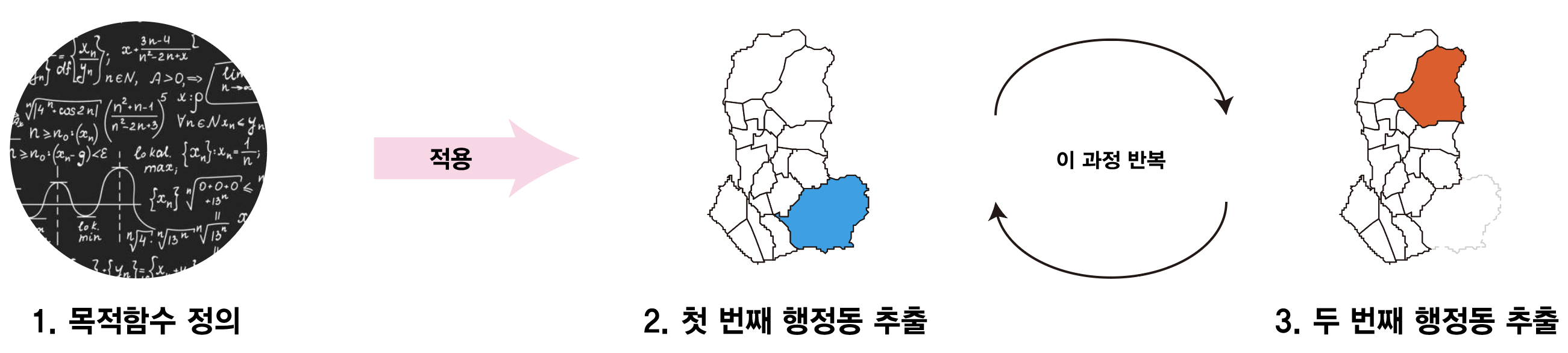
먼저 위에서 정의한 목적함수를 최대로 하는 첫 번째 행정동을 추출한다. 이후 첫 번째로 추출한 행정동을 제외하고 다시 MCLP 모델링을 적용하여 두 번째 행정동을 추출한다. 이 과정을 2 ~ 4회 반복하여 최종 접근성이 우수한 네 개의 행정동을 뽑겠다. 여기서 4개는 우리팀이 임의로 정한 자판기의 개수이다.
4. 교통편의성지수(\(C_{i, j}\)) 개발 및 적용
4-1. 행정동별 지하철 호선과 버스 노선 수 구하기
우선 정류장과 전철역을 shp파일에 Mapping하기 위해 ‘WGS84’인 좌표체계를 ‘UTM-K’로 바꿔주는 작업이 필요했다. 이후 Mapping된 자료를 통해 각 행정동에 속하는 지하철 호선과 버스 노선 수를 파악했다
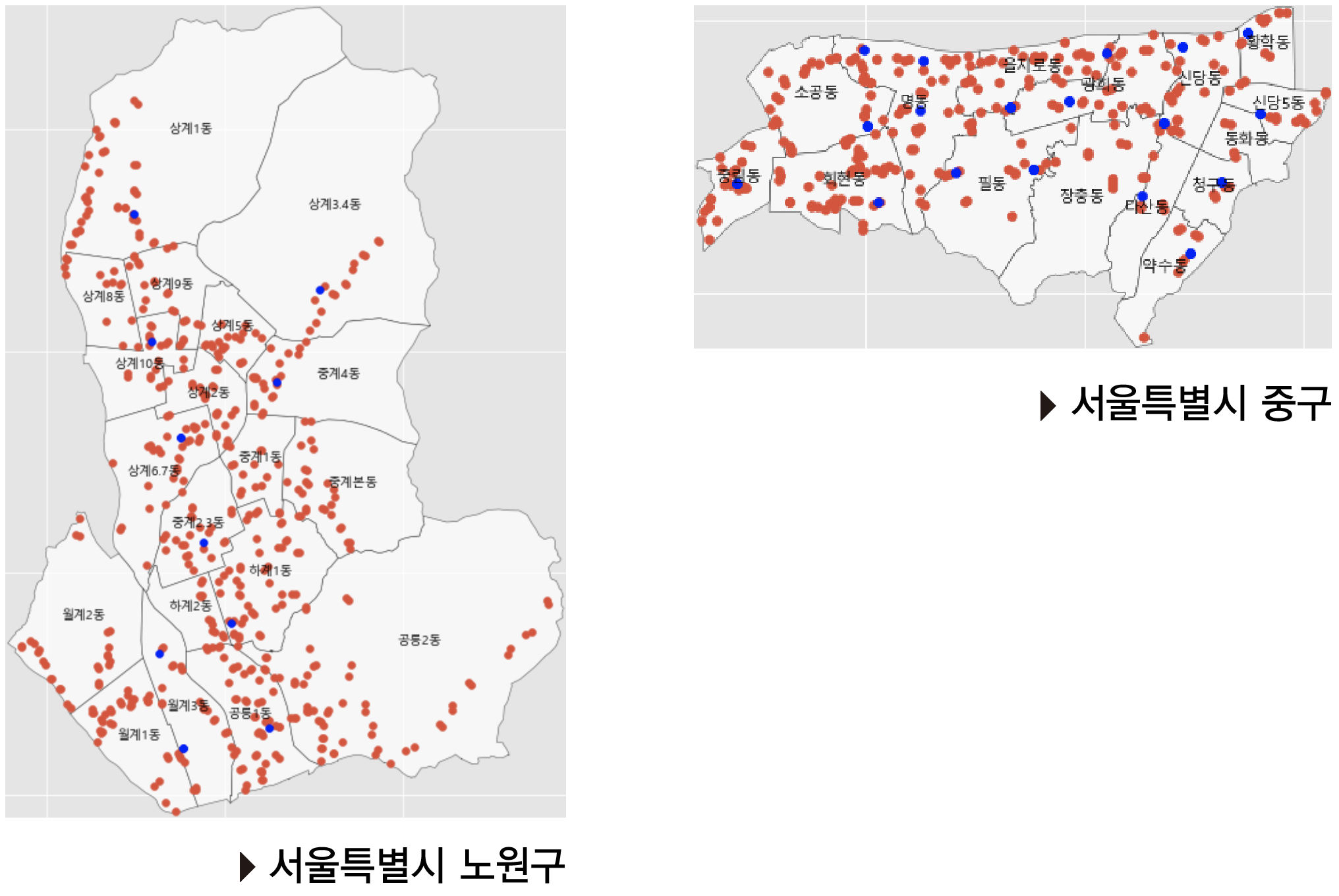
여기서 아쉬웠던 점은 대구지역 생활인구 데이터를 구할 수 없기 때문에 부득이하게 서울 중구와 노원구 만을 대상으로 분석을 진행했다.
4-2. 행정동 간 교통편의성 지수(Conv_out)
교통편의성 지수를 더 세밀하게 구하기 위해서 교통편의성 지수를 ‘행정동 간 교통편의성 지수’와 ‘행정동 내 교통편의성 지수’로 나누어 좀 더 세밀하게 분석했다.
| \(Conv\_out\) 행렬 | \(Double\,Power\,Distance\,Weights\) |
|---|---|
 |
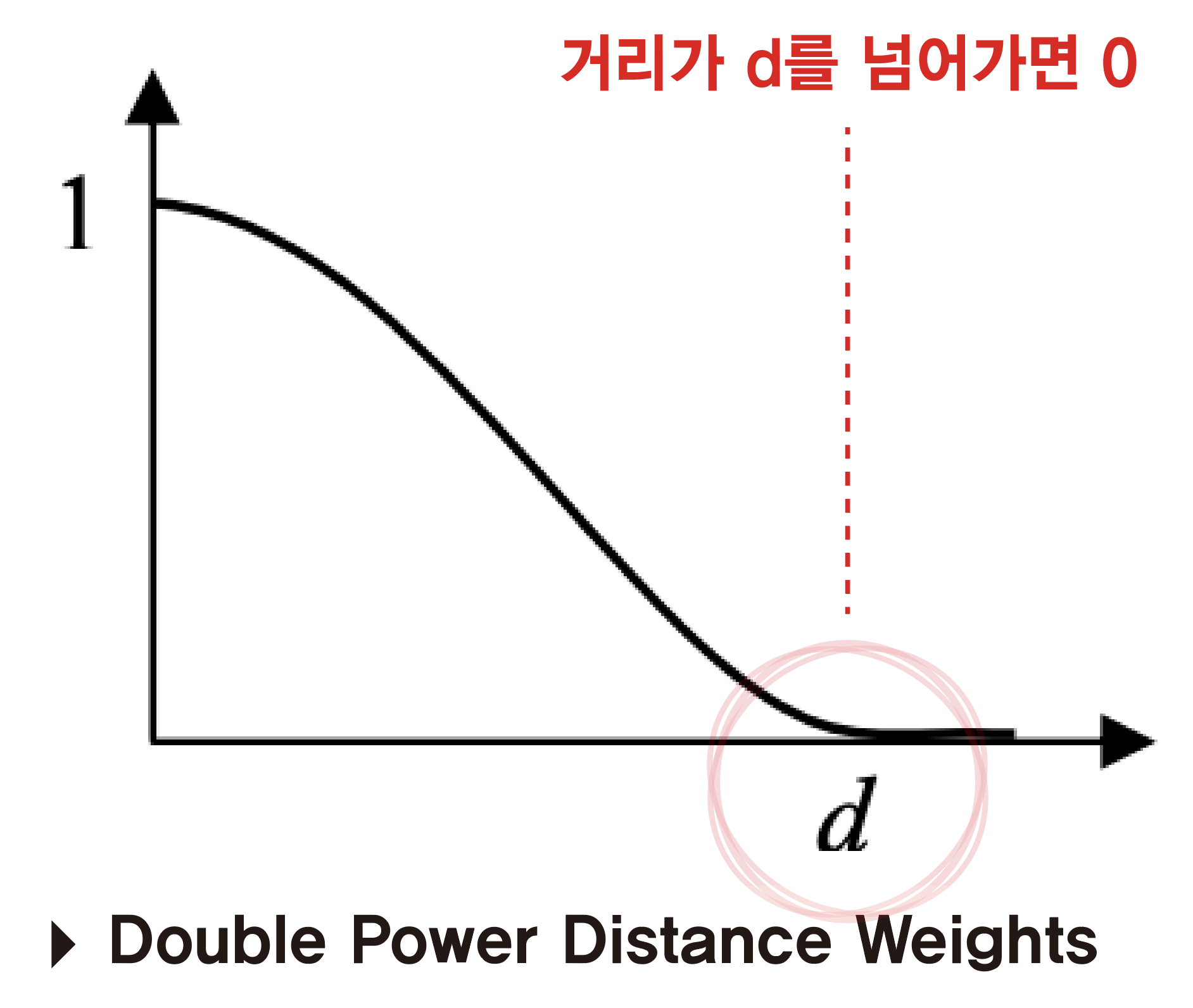 |
\(Conv\_out\) 행렬은 행정동 간 교통편의성 지수로 대각원소가 0인 행렬이다. 행정동과 행정동을 연결하는 교통수단(지하철, 버스)이 많을 수록 행렬값이 커진다. 또한 행정동 간 가까운 정도를 구할 때 ‘Double Power Distance Weights’를 사용하여 거리에 따라 가중치를 주되, 행정동 간 거리가 일정 수준(d)을 넘어서면 교통편의성 지수를 0으로 할당한다. 여기서 d는 노원구와 중구의 행정동 중심간 평균 거리가 2.6km인 것에 근거해 3km로 설정하였다.
4-3. 행정동 내 교통편의성 지수(Conv_in)과 교통편의성 지수 최종 행렬
| \(Conv\_in\) 행렬 | 최종 \(Conv\) 행렬 |
|---|---|
 |
 |
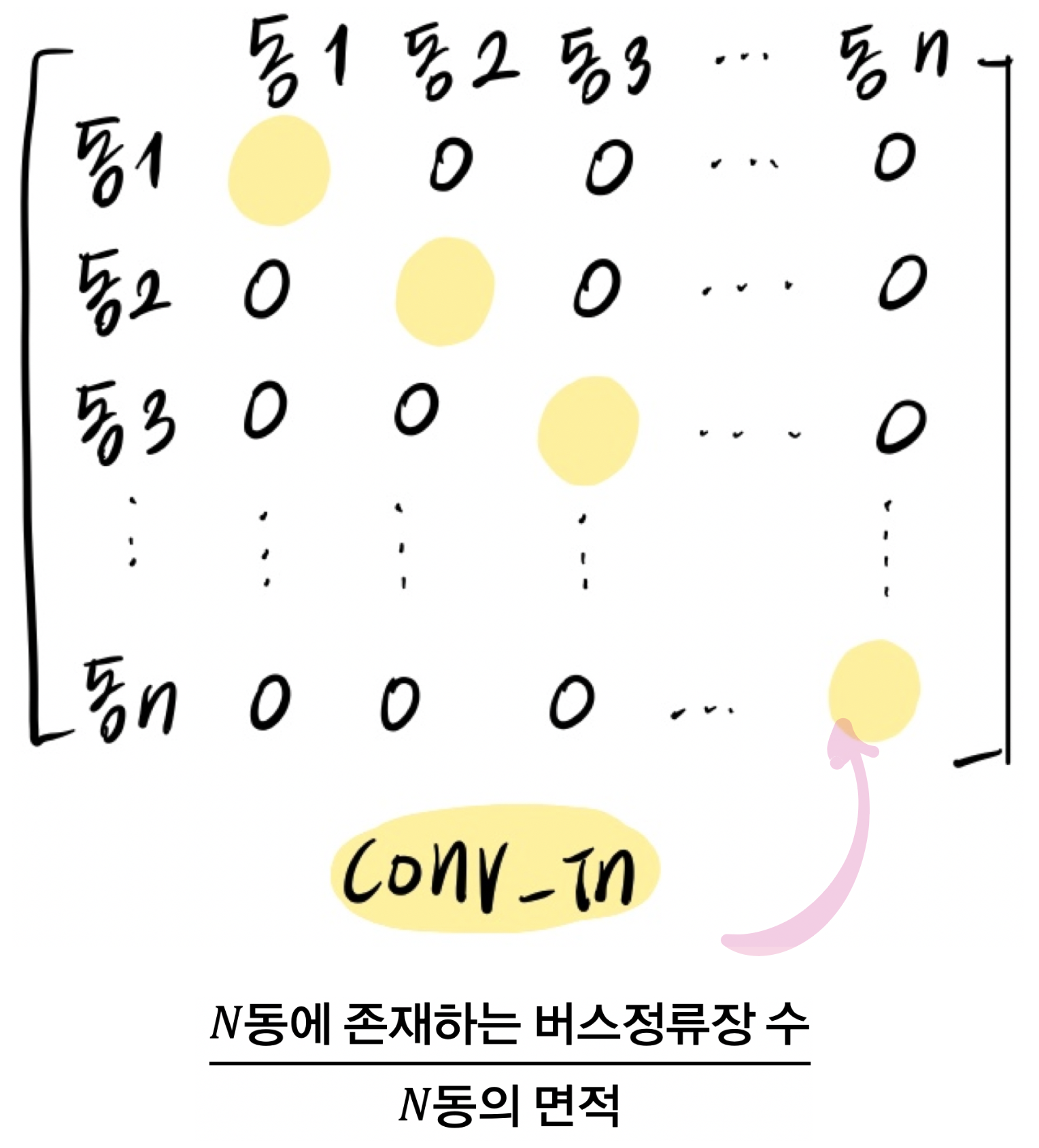
\(Conv\_in\) 행렬은 행정동 내 교통편의성 지수로 \(N \times N\) 대각 행렬이다. 중구와 노원구의 행정동 내 평균 지하철역 개수가 0.86개(노원구 0.52개, 중구 1.2개)로 1개 미만이다. 따라서 행정동 내 생활 인구 이동은 버스를 수단으로 삼는다는 전제 하에, \(Conv\_out\)과는 다르게 지하철역 데이터는 제외하고 교통편의성 지수를 설계했다.
마지막으로 최종 교통편의성 지수인 \(Conv\) 헹렬은 \(Conv\_out\) 행렬과 \(Conv\_in\)행렬을 더함으로써 생성했다.
- \[Conv = Conv\_out + Conv\_in\]
\(Conv\_out\) 행렬 상세
- \[D_{n,n} = \{d_{i,j}\} \ s.t\ \ d_{i,j} = \begin{cases} \left (1-\left (Dist(h_i,h_j) \over d \right)^2 \right )^2 & \text{if $0 \le Dist(h_i,h_j) \le d $} \\ 0 & \text{if $Dist(h_i,h_j) > d$}\end{cases}\]
- \[R_{n,n} = \{r_{i,j}\}\ s.t\ \ r_{i,j} = \begin{cases} \sqrt{\left ({bus\ route (h_i,h_j) \over total\ bus\ route} \right)} + \sqrt{\left ({subway\ route (h_i,h_j) \over total\ subway\ route} \right)}& \text{if $ i \ne j$} \\ 0 & \text{if $ i=j $}\end{cases}\]
- \[Conv\_Out_{n,n} = D_{n,n} \odot R_{n,n} \quad (elementwise\ multiplication\ of\ D_{n,n}\ \text{$and$}\ R_{n,n})\]
\(Conv\_in\) 행렬 상세
- \[C_i = {number \, of \, Bus \, Stop \, in \, h_i \over AREA(h_i)}\]
- \[Conv\_in_{n,n} = \left[\begin{array}{ccc} C_1 & & \\ & \ddots & \\ & & C_n \end{array}\right]\]
4-4. \(Conv\) 행렬 최종 결과 예시
위의 공식만 봐서는 \(Conv\)행렬의 최종 형태가 와닿지 않는 분들도 계실거라고 생각한다. 따라서 \(Conv\)행렬 예시를 첨부하겠다.
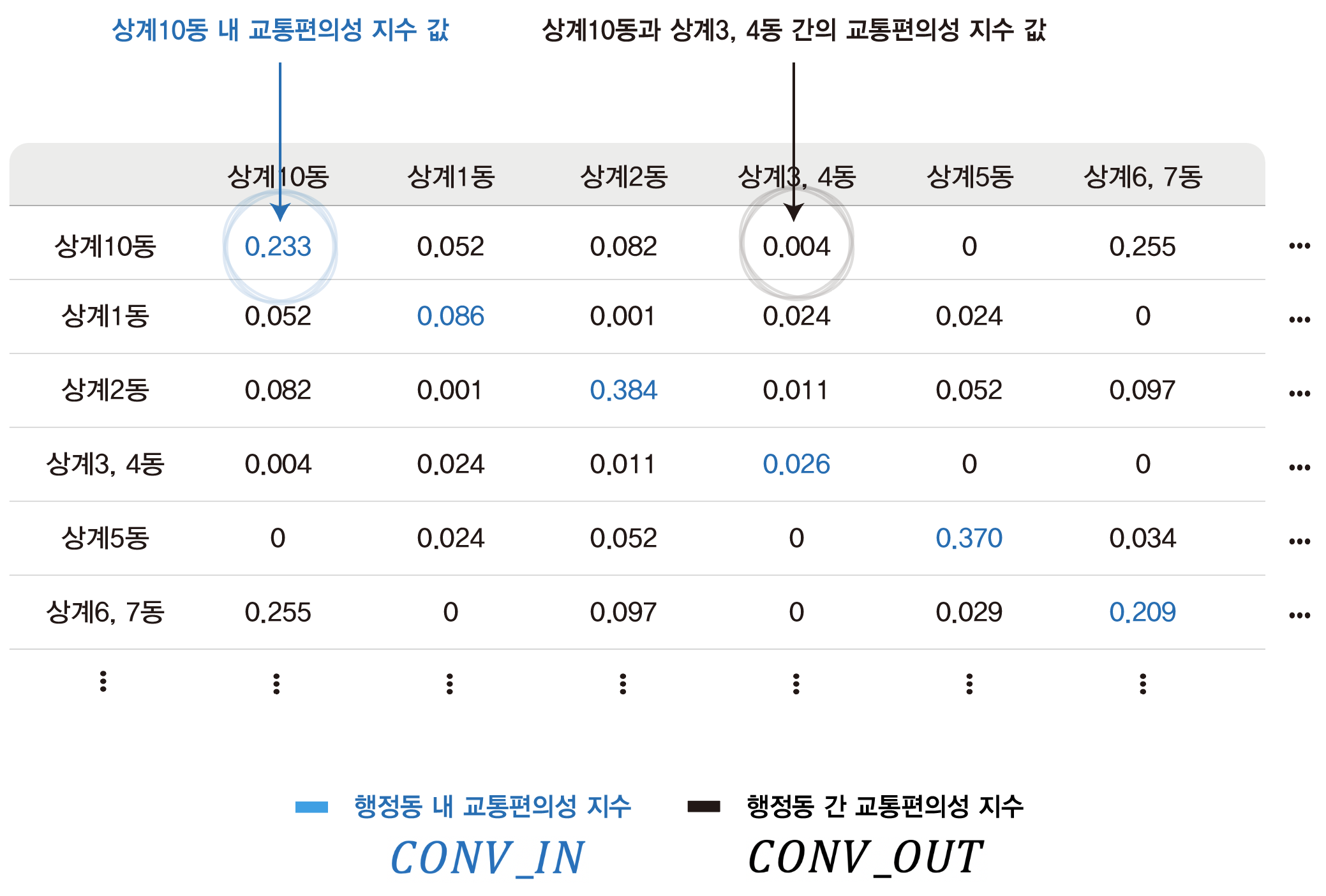
이제 교통편의성지수에 대한 설명은 끝났다. 다음으로 볼 것은 \(Conv\)행렬을 이용하여 행정동별 거리 가중치 행렬인 \(W\)행렬을 구하는 과정이다.
5. 행정동별 거리 가중치 행렬 \(W\) 구하기
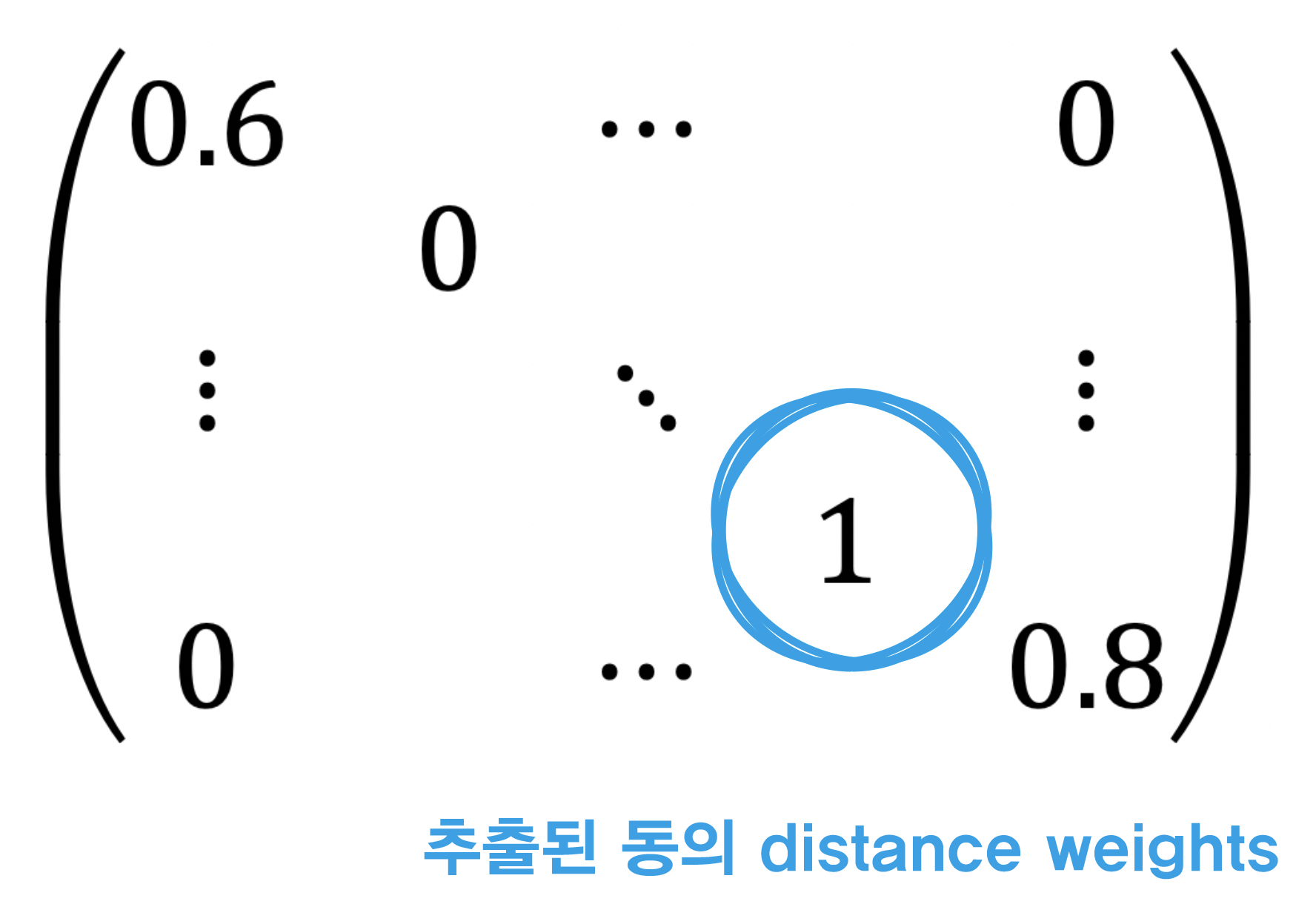
이 과정을 이해하기 위해서는 MCLP의 목적을 이해하는 것이 중요하다. ‘MCLP는 제한된 시설물의 개수로 최대 수요를 예측하는 모델링이다.’ 모델링의 목적에 맞춰서 생각해자. 첫 번째 MCLP 수행을 통해 A라는 행정동이 나왔다고 가정하자. 그럼 A 행정동의 인접 행정동은 시설물의 수요에 이미 들어간 것이나 다름없다. 즉 다음 행정동을 뽑을 때 A행정동과 거리가 먼 행정동을 뽑아야 더 많은 지역 수요를 충족시킬 수 있다는 것이다. 따라서 위에서 나온 \(Conv\) 행렬에 \((1\, - \,distance \,weights)\)를 처리해주어 거리 가중치의 크기를 역전시켜줘야 MCLP 모델링을 올바르게 적용하는 것이다.
| 전 처리 전 \(W\) 행렬 | 전 처리 후 \(W\) 행렬 |
|---|---|
 |
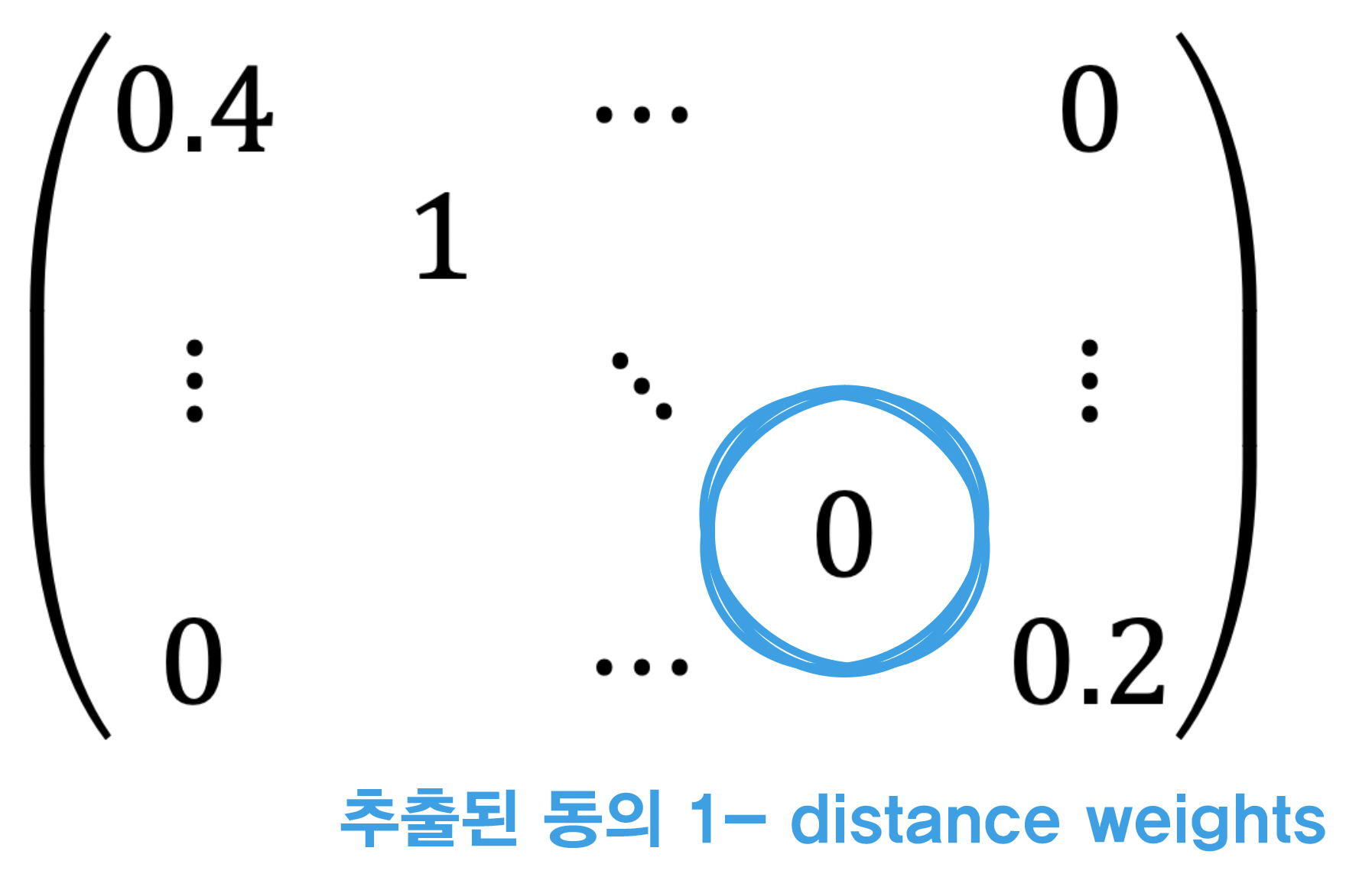 |
\(W\)행렬의 크기를 반전시켜줌으로써 새롭게 자판기를 설치할 행정동을 뽑을 때 이미 자판기가 설치된 행정동의 영향을 최소화 하였다. 다시말해서, 전에 A 행정동에 자판기가 설치 되었다면, 다음번 행정동을 추출할 때에는 A 행정동과 적당히 먼 행정동을 고르게끔 했다는 것이다. 이를 통해 한정된 자판기의 수요로 최대 지역 생활인구를 커버할 수 있도록 하였다.
6. 주중/주말 생활인구 파악 및 가중치 계산(\(L_{i, 1}\))
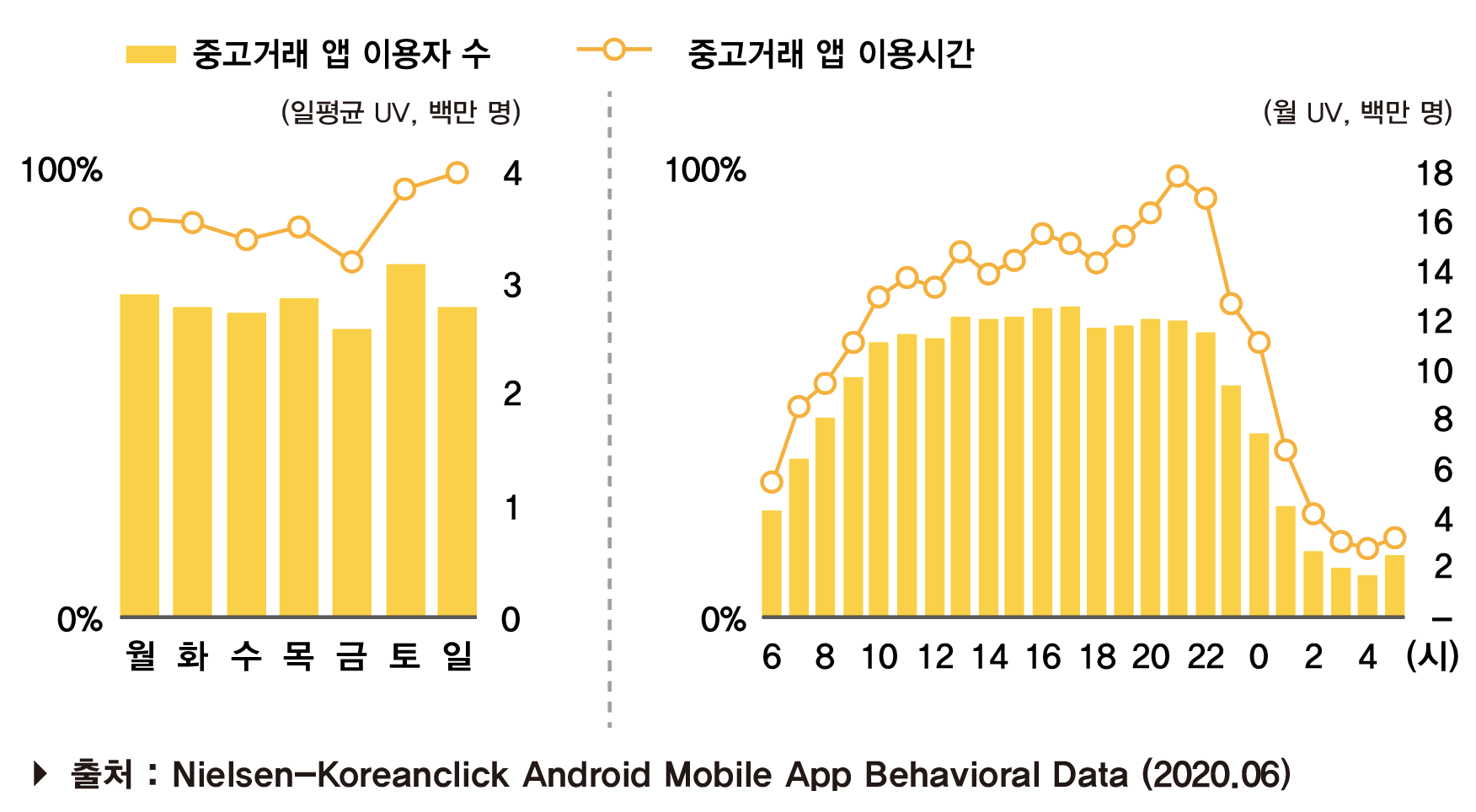
MCLP 모델링의 교통편의성지수 \(C_{i, j}\)에 이어서 행정동별 주말•주중 생활인구 가중치인 \({L_{i, 1}}\)을 구해보겠다. 먼저 우리팀이 MCLP 모델링을 하는 이유는 자판기 플랫폼이 최신 뉴노멀 트렌드인 ‘중고거래’트렌드를 잘 수행하도록 만들기 위함이다. 따라서 중고거래앱 사용성 통계를 이용해 주말과 주중의 가중치를 간단하게 구해봤다.
| 중고거래앱 사용성 통계 그래프 | 평일, 주말 생활인구 그래프 |
|---|---|
 |
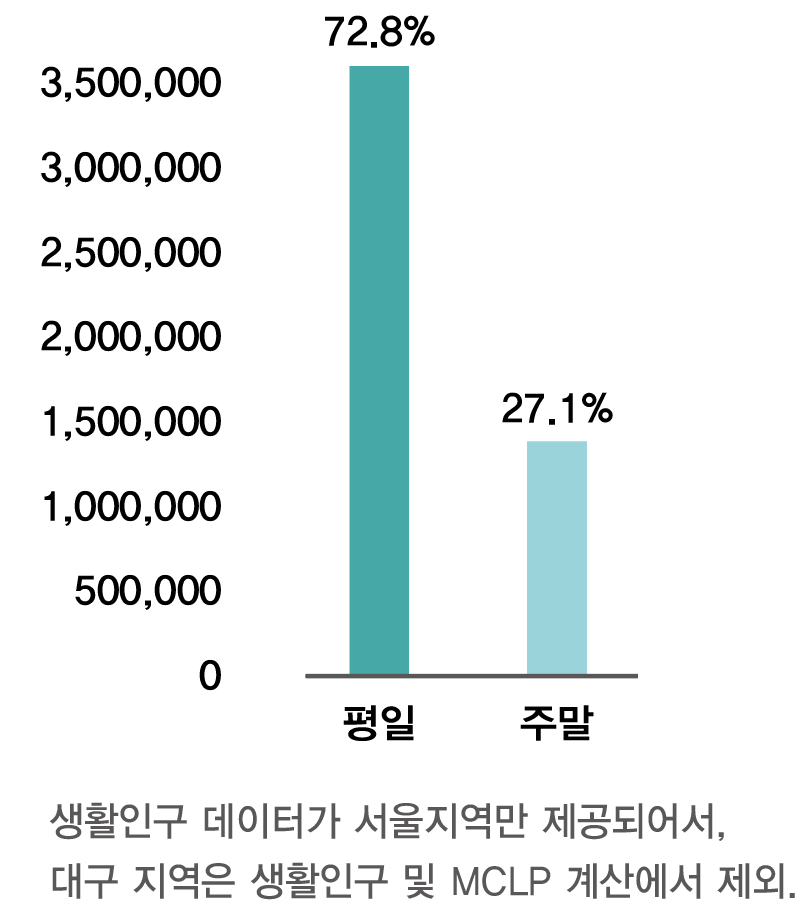 |
중고거래앱 사용 통계를 살펴본 결과 평일과 주말의 이용자 수는 유의미한 차이를 보이지 않았다. 그러나 이용시간은 확실히 주말이 더 긴 것을 확인할 수 있었다. 또한 사람들은 오전 9시부터 오후 9시까지 중고거래앱을 많이 사용하는 것으로 밝혀졌다. 이를 근거로 오전 9시부터 오후 9시까지의 서울지역(노원구, 중구) 평일, 주말 생활인구를 살펴본 결과 전체 생활인구 중 72.8%가 평일 생활인구, 27.2%가 주말 생활인구로 밝혀졌다.
따라서 행정동별 주말과 주중 생활인구 비율이 0.73:0.27이지만 주말에 중고거래앱 사용 시간이 더 긴 것을 고려하여 ‘평일 생활인구 가중치를 0.7, 주말 생활인구 가중치를 0.3’으로 정하였다.
7. MCLP 목적함수 최종 계산 및 결과
MCLP 계산을 위한 교통편의성 지수 행렬, 거리 가중치 행렬, 생활인구 가중치 행렬이 다 만들어졌다. 이 세가지 행정동을 행렬곱하여 최종 행정동별 목적함수 값을 추출해낸 후 이 목적함수 값을 기준으로 자판기의 최종 입지 선정을 진행하겠다.

7-1. MCLP 행정동 추출 결과
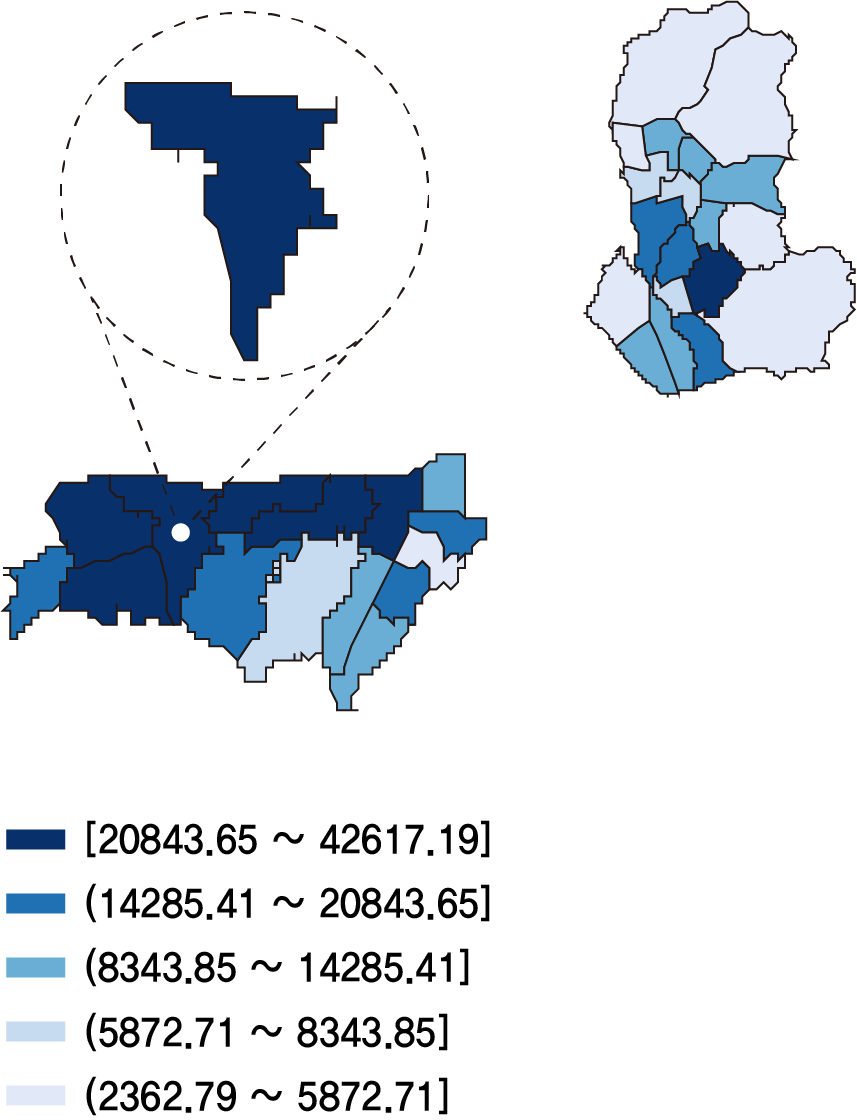
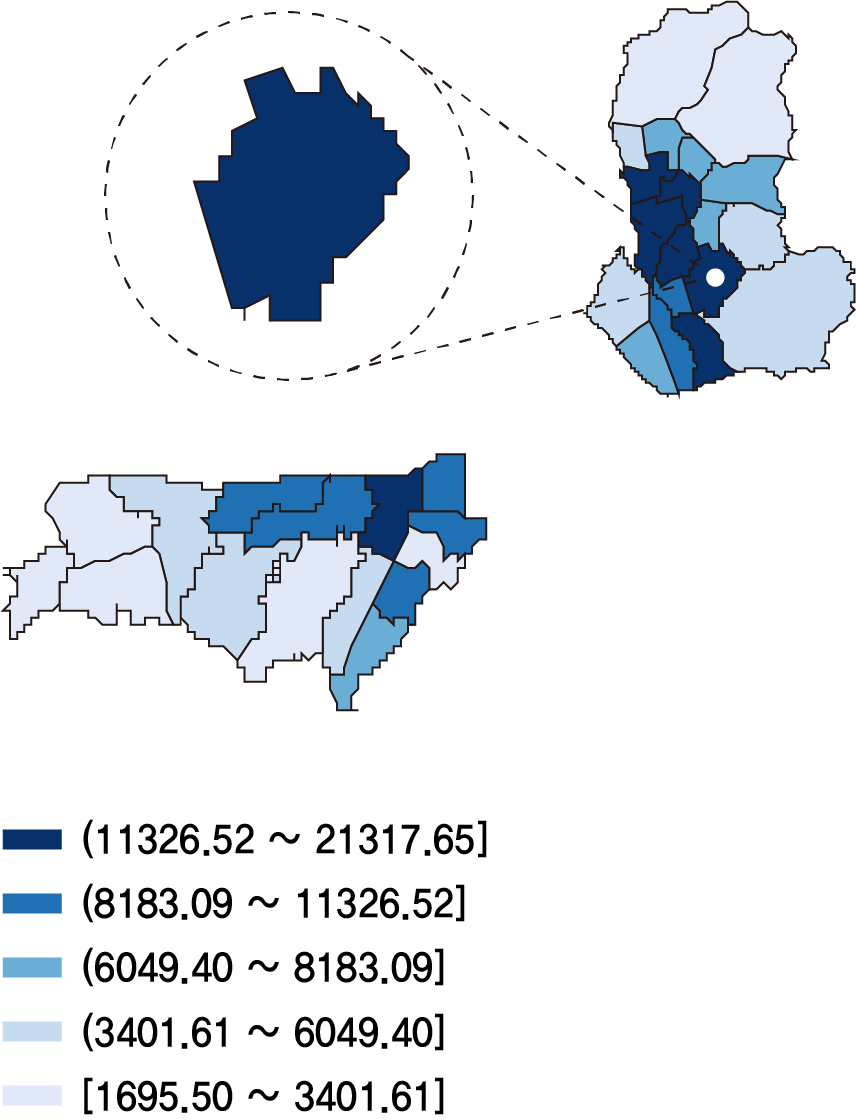
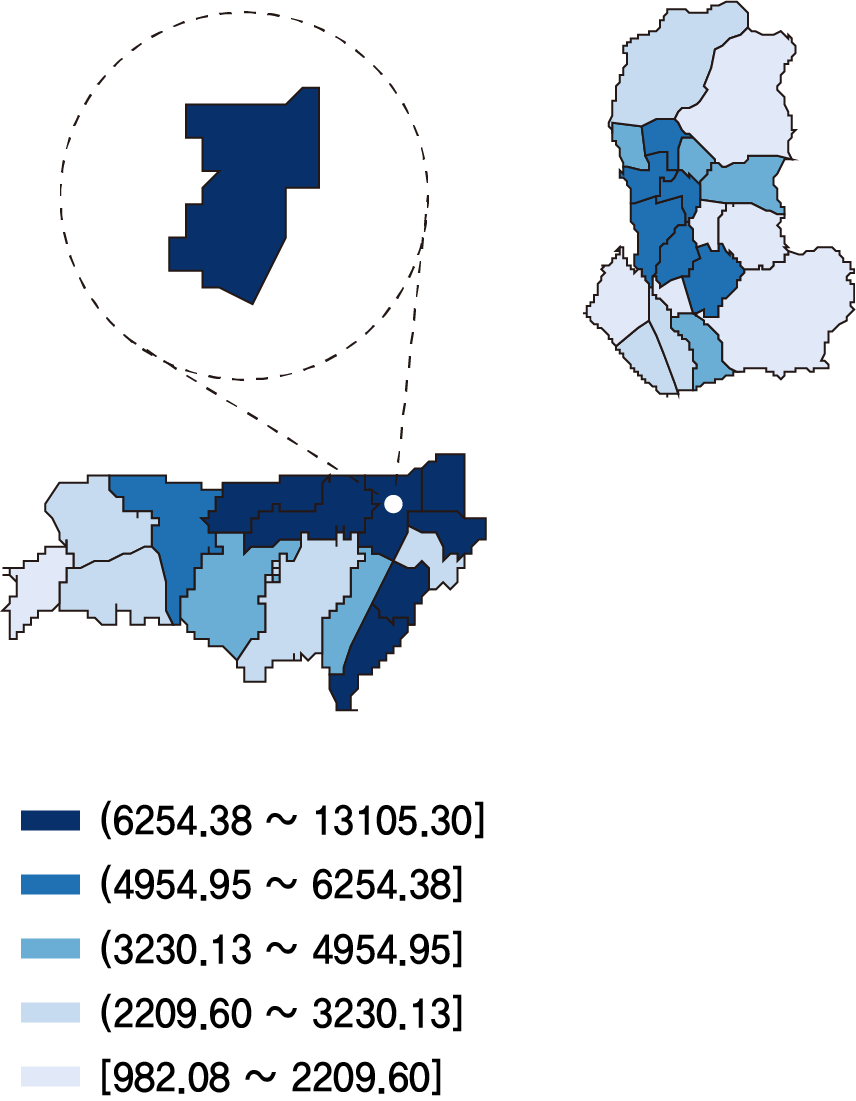
| 1st_명동(중구) | 2nd_하계1동(노원구) | 3rd_신당동(중구) | 4th_상계6,7동(노원구) |
|---|---|---|---|
 |
 |
 |
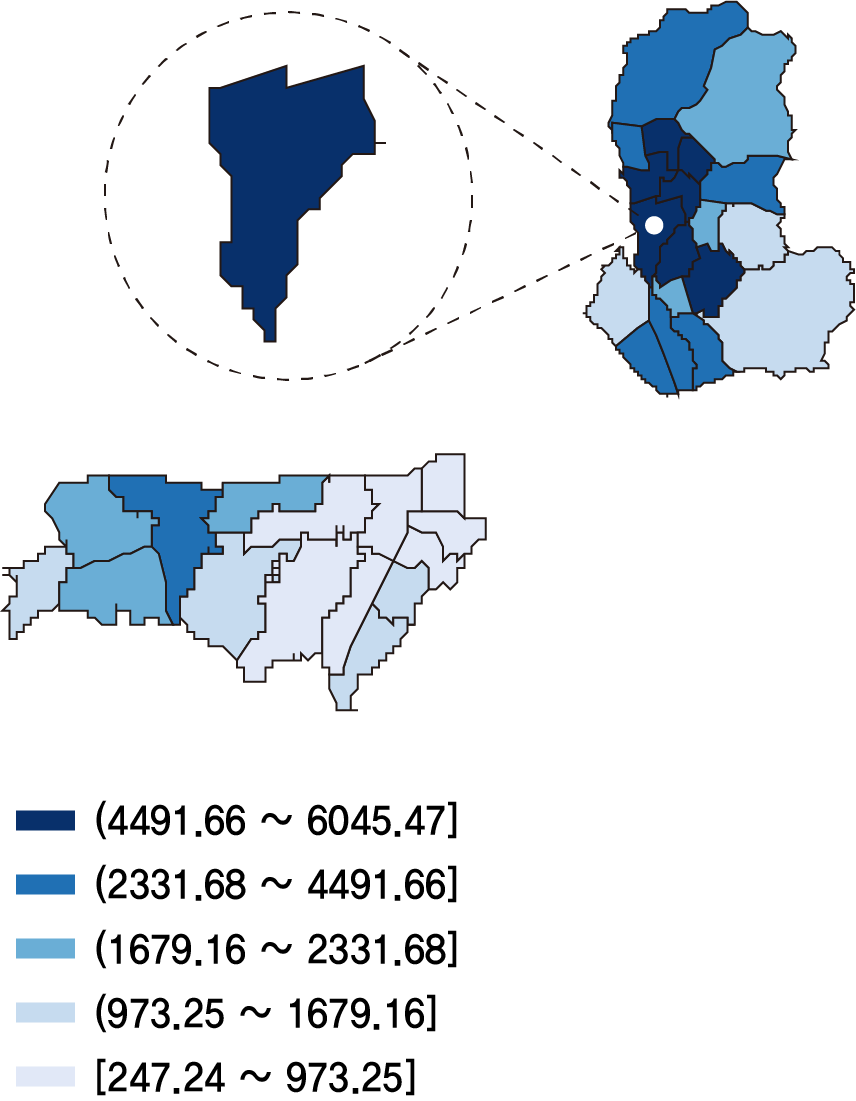 |
MCLP 모델링 결과 명동, 하계1동, 신당동, 상계6,7동 순으로 의류 중고거래를 위한 자판기 설치 최적 행정동으로 나왔다. 이 네 개의 행정동 중에서 테스트베드를 선정하기 위해 중고거래 서비스인 번개장터의 의류 카테고리 매물건수 크롤링을 진행했다.
| 번개장터 의류 카테고리 크롤링 결과 그래프 |
|---|
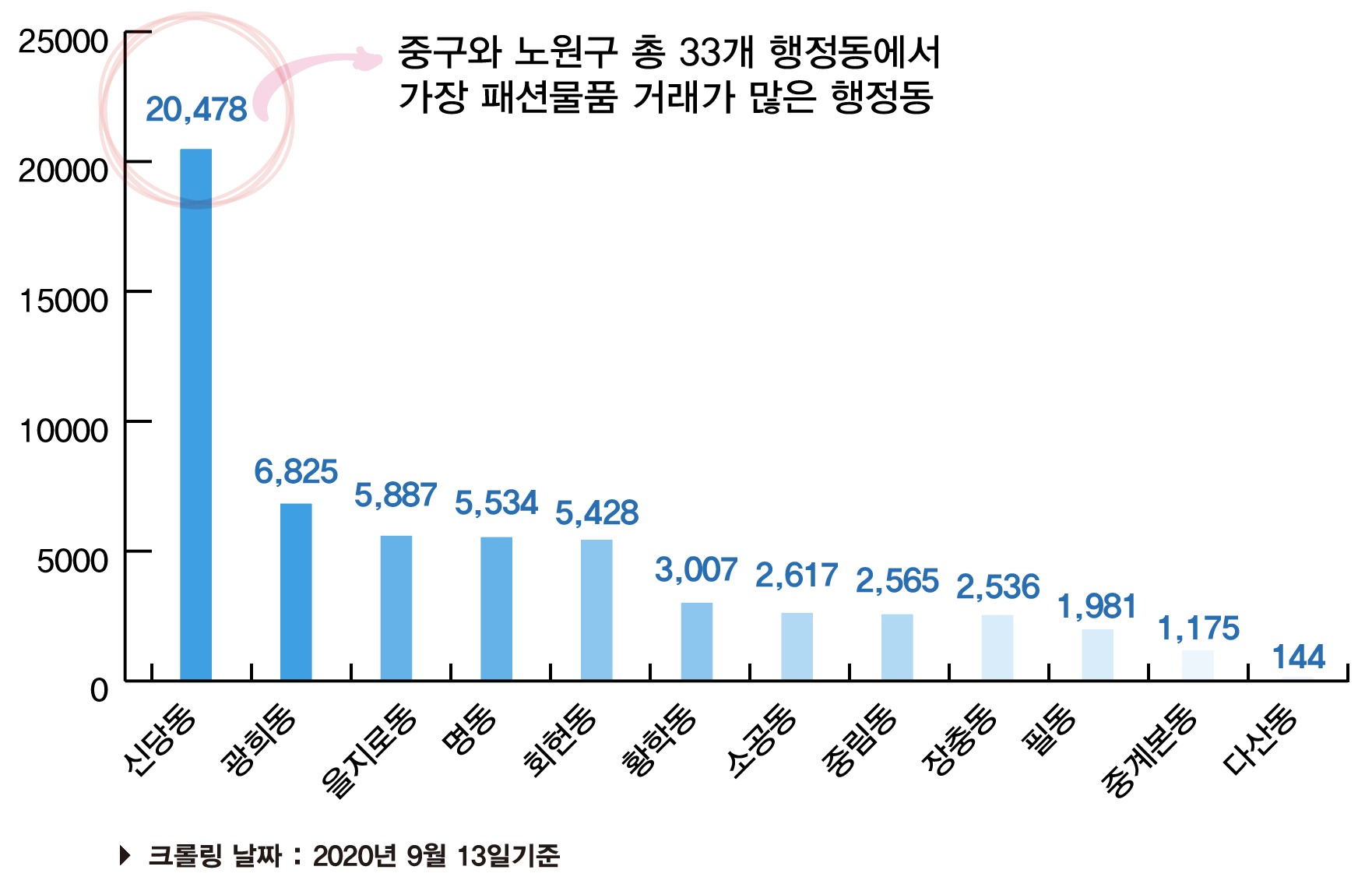 |
번개장터 의류 카테고리 크롤링 결과 2020년 9월 13일 기준으로 신당동의 물품건수가 20,478개로 다른 행정동에 비해 압도적으로 많음을 알 수 있다. (매물건수가 100이하인 행정동은 그래프에 표시하지 않음) 이를 근거로 중고거래 의류 자판기를 신당동에 설치하면 사람들에게 어느정도 수요가 있을 것이라 생각한다.
7-2. Space Syntax를 통한 신당동 세부 위치 선정
그렇다면 신당동 내 구체적으로 어떤 위치가 자판기를 설치하기에 가장 최적의 위치일까? 이를 알아보기 위해 공간 구조의 속성을 정량적으로 분석하여 공간의 상호관련성과 특성을 파악하는데 주요한 기법인 Space Syntax를 사용하여 신당동에서 가장 접근성이 좋은 동선을 뽑아내었다.
| 신당동 Space Syntax 결과 | 실제 지도위에서의 동선 위치 |
|---|---|
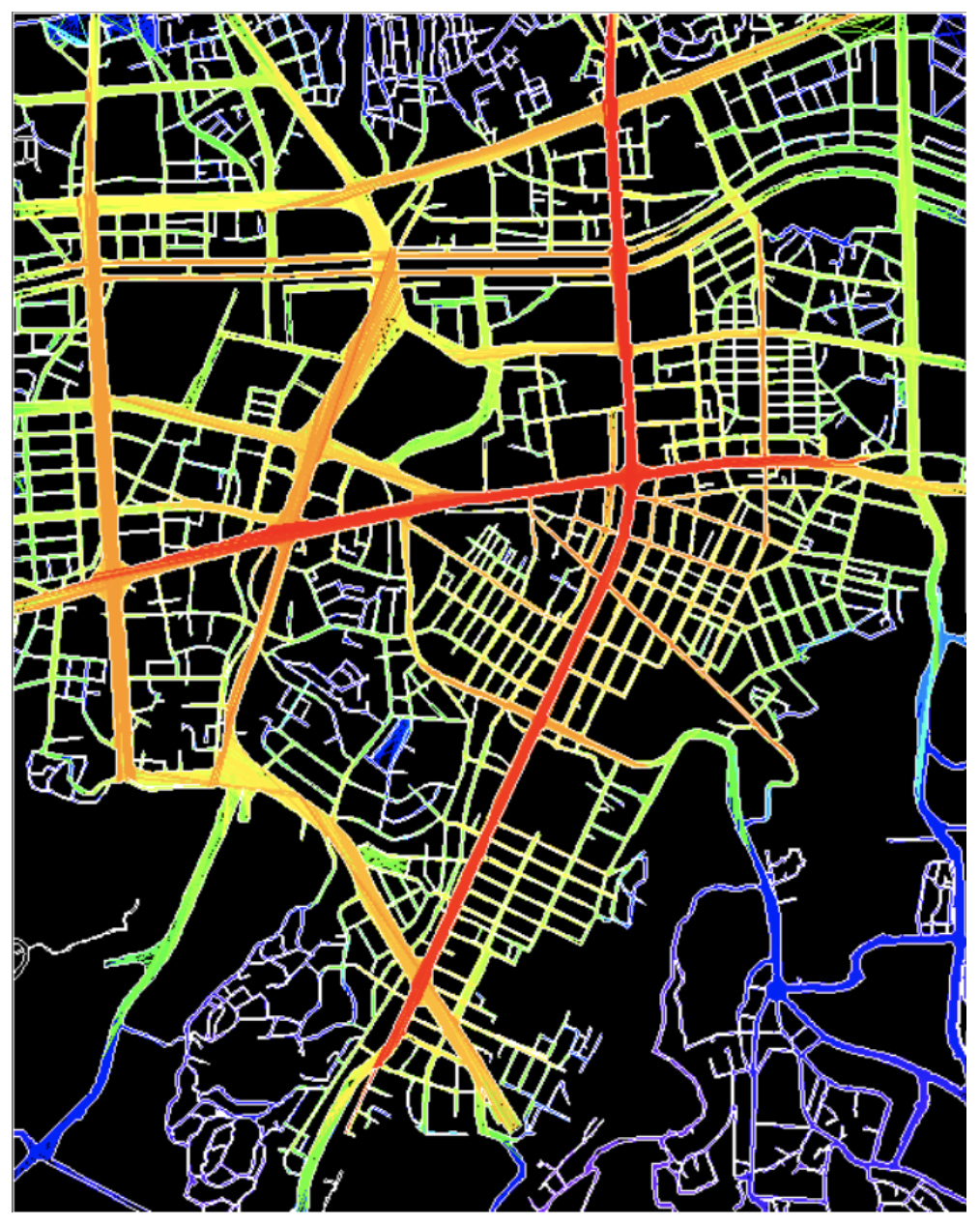 |
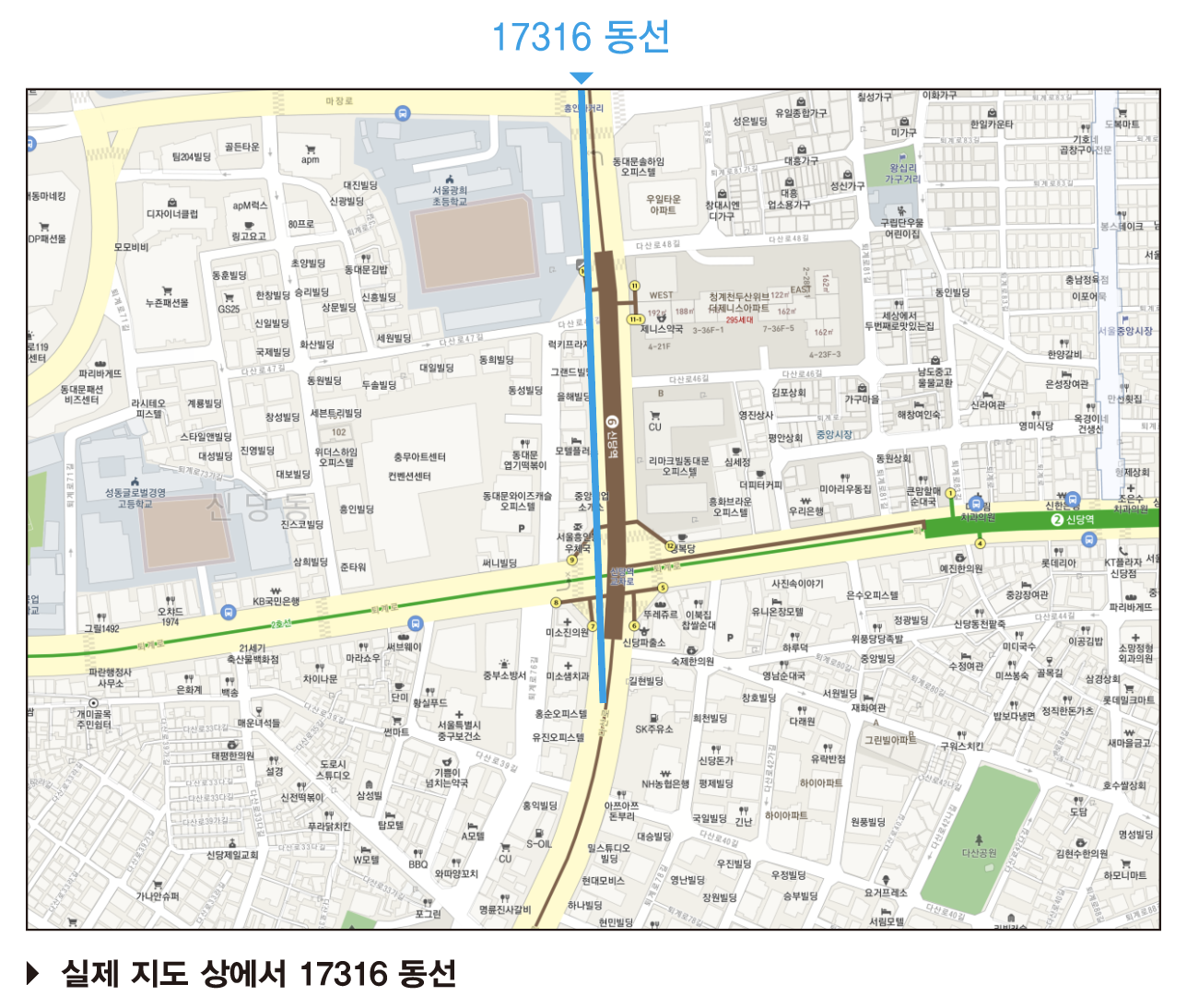 |
신당동 Space Syntax 분석 결과 ‘신당역 교차로’부분이 가장 접근성이 뛰어난 곳인 것으로 밝혀졌다. 신당역 교차로 주변에는 DDP, 충무아트센터 등 유명 명소가 많아 더욱 최적의 위치임을 실감할 수 있다.
8. 어떤 중고 패션 자판기를 만들 것인가?
길고 긴 포스팅에서 우리는 네 가지 Index를 통해 ‘패션’이라는 업종을 뽑았고, MCLP 모델링과 Space Syntax를 통해 ‘신당역 교차로’라는 자판기의 최적 위치를 설정했다. 이제 남은건 자판기의 컨셉이다. 뉴노멀 서비스 트렌드인 ‘중고거래’, ‘비대면’, ‘체험형’을 만족시키는 자판기 컨셉으로는 무엇이 적합할까?
| 최종 자판기 컨셉 |
|---|
 |
우리팀이 생각한 자판기 컨셉은 다양한 인공지능 서비스를 이용해 신선한 체험을 할 수 있는 의류 자판기이다. 자판기에 AR 기능을 추가해 사람들이 옷을 고르면 실제로 옷을 입어보지 않고 가상으로 입어보도록 하거나, 사람들에게 얼마나 어울릴지 판별해주는 것이다. 마치 ‘아마존의 에코룩’서비스가 했던 것처럼 말이다.
또한 자판기에 스타일러와 같은 부가적인 기능을 추가하여 소비자들에게 항상 최상 품질의 옷을 제공해주면 매력적일 수 있을 것이라 생각했다. 그러나 단점은 언제나 그렇듯 기술의 한계이다. 현재 AR 기능의 수준으로는 사람들이 체감할 수 있을만한 서비스 환경을 구축할지 미지수이기 때문이다.
그러나 현재 여러 산업에서 벌어지고 있는 ‘분산화(탈중앙화)’, ‘언택트’ 등의 신드롬을 미루어 보았을 때, 이런 자판기 서비스는 언젠가 우리의 생활 밀접히 들어오게 될 것이라고 생각한다.
8. 공모전을 참여하면서…

약 두달간의 공모전을 참여하면서 정말 느낀 것이 많다. 먼저 내 스스로에게 느낀점은 디자이너로서, 기획자로서, 데이터 분석가로서 모든 면에서 실력이 부족하다는 것이였다. 멋진 자판기 외관 디자인과 멋진 기획, 멋진 분석을 하고 싶었지만 번번히 생각에만 그치고 실제로 수행하지를 못했다.
공모전을 할 당시에는 잘 수행하지 못한 이유가 시간과 데이터가 부족했기 때문이라고 생각했는데(어느정도는…), 공모전 기획안을 포스팅으로 옮기면서 분석이 논리적이지 않은 점, 기획이 참신하지 않은 점을 여실히 느끼면서 시간과 데이터의 문제가 아니라 내 문제인 것을 여실히 느꼈다.(아마 글을 보시는 분들도 띠잉? 하는 순간이 많았을 것이라 짐작한다.)
이제 스스로에게 느낀점이 아닌 공모전 전체로 느낀점은 ‘소문난 잔치라 먹을것이 많았지만 더 먹을게 많았으면 어떨까…‘이다. 그 이유는 약간의 데이터 부족이 느껴졌기 때문이다. 기업측에서 우리에게 준 것은 2019년과 2020년 2월에서 5월 약 4개월치 데이터이다. 공모전이 나온 시점이 9월인 것을 미루어 보아 5월까지가 아닌 7월까지정도는 주셨으면 어땠을까 하는 생각을 해본다.
또한 코로나 이후의 기간인 2020년과 비교대조 할 수 있는 년도가 2019년밖에 없었다. 그렇기에 분석을 하면서 ‘2019년으로 과거 모두를 일반화해도 될까?’라는 생각을 스스로에게 많이 던졌다. 2018년, 2017년 이렇게 3년치 정도를 줬으면 더 좋지 않았을까 생각해본다.
그러나 너무 좋은 공모전이었다. 개인적으로 주제도 너무 재밌었고 준비하면서 많은 공부를 했던것 같다. 아직 결과는 어떨지 모르겠지만 그래도 소중한 포스팅 컨텐츠를 건졌으니 이미 반 이상은 성공한 것이라고 생각한다. 그럼에도 불구하고 사실 상은 받고싶다!
끝으로 빨리 코로나가 종결되고 마스크를 끼지 않는 평범한 일상으로 돌아가고 싶은 마음이 공모전 분석 내내 들었다. 하루빨리 관중이 꽉찬 EPL을 볼 수 있길 희망하며 빅콘테스트 포스팅을 마무리 짓겠다. 긴 글 읽어주신 분들 너무 감사드립니다! 피드백은 댓글로 남겨주세요!